Mechanics and Technology

All mechanics is based on solids (or sufficiently compressed matter). Mechanics deals only with materials (atoms, molecules) in the solid state. Where there are no solids no rigid bodies, there is no mechanics. You might argue what about hydromechanics or aeromechanics – the flow of air, gases and vapours. Try calculating the flow of a liquid or gas in a completely free space. I repeat in completely free space, without tanks, channels, without earth’s gravity in the atmosphere or magma flow inside the earth, etc. You don’t count anything, or you count everything as you please. Because there are no given boundary conditions – pipe, tank, room volume, water reservoir, gas reservoir, atmospheric envelope of the earth, etc. The boundary conditions are just determined by the solid phase, I’m leaving out Jupiter and the stars, there their boundary conditions are determined by gravity and the different ratios in different parts of those bodies.
In short, hydromechanics (liquids) and aeromechanics (gases) depend on boundary conditions either in the form of classical solid envelope or gravitational forces (rarely electromagnetic forces).
Notice: Also, all organisms are given by solids (along with liquids and gases). There is no organism that consists only of liquids and gases.

Solids are given by chemical elements in solid state like Fe, Sn, Cr, Cu, etc. or their alloys, mixtures or compounds thereof. Their mechanical properties (stress, strain, strenght, elasticity, etc) are given by intolerance of electrons in their atomic shells. All material sciences with their elasticity, plasticity are given by exclusion principle. But it is not enough. 

Let´s go to interesting elasticity, especially spring elasticity

Here we have four examples of elastic behaviour in mechanics. We suppose absolutely rigid the ball, the wall and the construction. Reference system is outside – connected with “paper”. See images below.

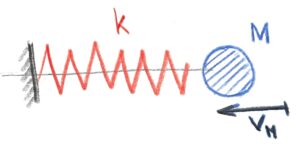
The first example is clear – a ball with mass M1 moving with velocity vM1 against a fixed rigid wall with a spring of stiffness k.

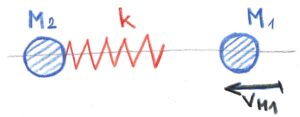
The second example is similar to the first with the important difference that the fixed stationary wall has disappeared and instead there is a standing ball with mass M2.

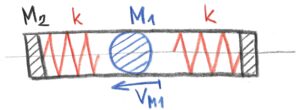
In the third and fourth examples, a ball with mass M1 is enclosed in a rigid closed construction with mass M2
The third and fourth examples look the same, but are not the same. The difference between initial conditions.
In the third example, the ball with mass M1 has an initial velocity vM1, while the closed rigid construction with mass M2 is standing. Both left and right springs with the same stiffness k are free – not compressed.

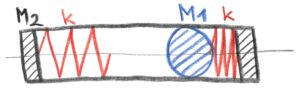
In the fourth case, both the ball with mass M1 and the structure with mass M2 are initially standing. The right spring with stiffness k is maximally compressed. The left spring with stiffness k is free.

Next, we will solve the measurement of motion in the previously mentioned examples with respect to the reference system. This is in the case where we replace the photons with mechanical balls of mass m with velocity v. The problem is the so-called rest mass of the bodies. We know very well that there is no ideal rest system in the world. Neither is an ideal rest mass.

In the first case we have to solve the problem of ball impact to spring. To solve the duration of impact, the maximall compress of spring and, if we please, the progression of velocity and acceleration of the ball. Firstly I must write – to solve upper case is impossible in the real world. We must this case make easy – to simplify it. To take out the case from the world. To idealize the case. Ignore all irrelevant details. But the case is given by the world. This case can not exist without the world in the same way like organisms – tear off the flower and study it, especially its living processes. Nothing against simplification, but don´t remember it our model has its own limitations.

Initial conditions:
The ball with mass M with inital velocity v in the direction of the axis x of the spring, the weightless spring with a stiffness k, the fixed wall – it is also our reference point.

To solve only max. compress of the spring – it´s easy.
We use only two fromulas – first of them for kinetic energy Ek of the moving ball Ek=1/2Mv^2

the second one for potential energy Ep of compressed spring  
Ep=1/2kx^2

from the law of conservation energy Ek = Ep after that we are able to solve the max. compress x max. of the spring.

the solve the duration of impact and the progress of velocity or deccelleration and accelleration we must use the classical mechanics consideration about the force between ball and the spring

the inertia force Fi = M*a

the “spring” force Fs = – k*x

these two forces are equall through the duration of the impact

Fi = Fs  then M*a = – k*x  or   M*a + k*x = 0

we are able to solve the accelleration a of the ball at any distance x from the beginning of the impact – we must use numerical methods, in the other hand to solve uppper case analytically we must use differential equations – where m represents mass M of the ball, a – accelleration, x – distance, k – stiffness, t – time

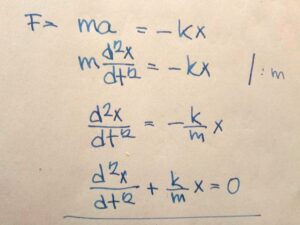
The results: functional dependence of distance on time x = f(t), x = C cos Ω t, where Ω^2= k/m and Ω*t=2*π . From here we can calculate the duration t of the impact.
The angular velocity Ω can also be expressed in units of seconds. Instead of the unit radian for angle, we use 1 as the unit of angle. In that case 1 means 360 degrees or 2*π radians. Thus angle 90° (π/2) will be 1/4,  then  angle 180° (π)  will be 1/2 and  angle 270° (3/4*π)  will be only 3/4 and finally the angle 360° (2*π) will be 1. So here we are at rounds per second. Generally cycles per seconds. A second, however, is defined as a certain number of wavelengths of selected radiation that serves as the basic unit of time. Then cycles of anything per base unit of time. For example, the number of different wavelengths per 1 selected (metric) wavelength. Or the number of events per 1 wavelength.

In the end we have got the succesfull model with results and, no doubt, such results are verified by measurement. What to wish for more. To solve the problem of elasticity? To find out hidden processes with verified model. To use our model for recognition of hidden processes connected with elasticity? Elasticity is the base of the universe. Without elasticity there could be only singularities (to close 0 or ∞ ). But elasticity needs a space. And the space needs matter – without matter there is no empty space. And matter (excitations of quantum field) needs time. And matter has the weight. To explain the subject of spacetimematter with our simplified models? Nothing against idealization, otherwise we wouldn’t do anything. We have to start somehow. But we need to go further. Correction about the unknown. That is the meaning of knowledge. 

A short note on the function of the coupled (connected) springs. There are two or more springs with their different stiffness, better written with their force (spring) constant k, then k1, k2, k3, … , kN
There are two basic possibilities how to connect the springs among them:
1) in series (i.e. in succession) Kc = k1 + k2 + k3 + … + kN
2) in parallel (i.e. side by side) 1/Kc = 1/k1 + 1/k2 + 1/k3 + … + 1/kN or Kc = k/N only for k1 = k2 = k3 = … = kN

If we connect 1000 springs in parallel with k = 1000 N/m , we get the total stiffness of the system Kc = 1 N/m. But this is valid for slow, gradual compression. The situation will be different with impact, because it depends on the speed of spreading of the impulse (impact) through connected springs.

Thermodynamics  – mechanics of chaotic behaviour of particles

The basis of thermodynamics and indeed of the whole world is chaos. Chaos in a closed space. Chaos of moving particles, molecules, atoms. This chaos can be converted into mechanical work by the controlled expansion of initially chaotically moving particles. See an engine piston or a turbine blade.

Let’s have a model – a closed box with N particles. Initial conditions – all particles have the same velocity. After some time we find that the velocities of the particles are different from each other. The speed of movement of particles in a closed space varies – from almost zero speed to maximum speed. There is a kind of average particle velocity that is close to the value at the initial conditions.

the velocity distribution of particles depends on :

– the volume of the box
– the size of particles (very interesting model with particles like ideal points with zero size – these never meet each other)
– the number of particles

particle size is relative to the size of the box

The rule is – the higher the speed – the shorter the duration. The same for the lowest speed. If we want to keep the lowest velocity or high velocity of a particle for a longer time – we would have to isolate the particle from other particles. Perhaps by expanding space or otherwise. See the rubber sheet thermodynamics in two dimensional space below.

See the image below – thermodynamics of rubber sheet, resp. of elastic membrane

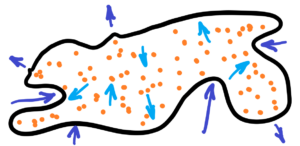
Thermodynamics of rubber sheet – elastic membrane full of chaotically moving particles. The disadvantage of isolating a particle is that we can keep its velocity for a longer time, but we cannot change it. Thus, it would be better to adequately stretch the elastic membrane according to how we want to accelerate the particle or, on the contrary, to decelerate it. Which leads to very interesting results.

Go back to thermodynamics before we begin to solve the thermodynamics of an elastic membrane or an elastic volume. How to describe purely chaotic processes? It is impossible to use mathematics. Mathematics doesn’t have a chance in the case of pure randomness. Mathematics has nothing to go on. But thermodynamics exists in clearly given mathematical equations. So the equation pV = nRT, very familiar equation for engineers. Sure, but there are differences. If we have one chaotic environment, we won’t be able to study anything, we won’t be able to describe anything, and we won’t be able to predict or verify anything. See first image below – only one chaotic environment.

So we need to have at least two different chaotic environments. One environment will be the chaotic motion of air molecules in the atmosphere and the other environment will be the chaotic motion of molecules in a closed cylinder with a piston. See a second upper image.
We will ignore temperature for the first time and examine what is called pressure and volume. It is possible to think like this and mainly to measure – volume and pressure – the weight of the mass relative to the given piston area. We obtain the equation p1V1 = p2V2. The multiplication of pressure and volume before expansion is equal to the multiplication of pressure and volume after expansion. Let us remember that we only know ratios and not absolute values. What is the absolute value of chaotic motion – relative to what? Relative to zero? Relative to what zero? To the zero of particles? But zero is not even in a vacuum – see the exclusion principle. Not to mention – relative to zero, everything is infinity!  And each unit we have chosen as the base unit of measurement is just a chosen ratio, the ratio between the measured value and the chosen (unit) value. Very important remark for next consideration in thermodynamics – expecially absolute temeperature, absolute pressure, absolute volume, absolute energy, absolute entropy, absolute enthalpy, etc. But the most important remark is about at least two chaotic environments with different characteristics to each other. For example, the expansion of the piston inside the steam cylinder, which is surrounded by dense, viscous oil , such expansion is different to the expansion of a piston inside a steam cylinder in an ambient atmosphere. Not to mention the change in the viscosity especially in the case of a non-Newtonian fluid.

See a cylinder with moving piston inside it. There are two different chaotical environments. See image below.

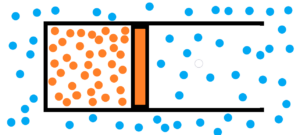
1) atmosphere filled with chaotically moving gas molecules – see blue dots
2) chaotically moving gas particles enclosed by a piston in the cylinder volume – see orange dots

Both the gas and the surrounding atmosphere are purely chaotic environments. In both environments, molecules collide. But in the case of a gas, we see that the collisions among gas molecules are more violent and more frequent compared to the molecules of the surrounding atmosphere. A gas enclosed by a piston in a cylinder will have tendency to expand relative to the atmosphere until the violence and frequency of collisions among the molecules are equal. Not to mention the final damping oscillations. See image below.

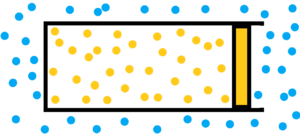
How to measure how to evaluate the violence and frequency of molecular collisions?
Some base units need to be chosen. See next image below.

To put a unit weight on the piston. How many units times the frequency and violence of collisions. At least for the beginning.

Rocket propulsion

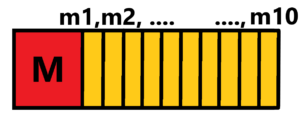
We will not discuss the theory of reactive propulsion arising from the law of conservation of momentum on the basis of third Newton´s law. At the beginning there is the mass of the rocket which is equal to M+m1+m2+ … +m10. Where M is nett weight of an accelerated satellite. While the sum of m1, m2, … , m10 is the weight of the fuel (propellant). When we want to accelerate a body M we have to rebound from something – the ground, water or air (propeller). We have nothing to rebound from in a vacuum. We need to take some propellant with us. And that’s a big problem – because of the maximum speed of the rocket. I mean, the more fuel we carry with us, the more fuel we have to burn. The only possibility is to increase the outlet velocity of the combusted fuel. The higher the velocity the higher the reaction for a given weight of fuel. 

There is a valid equation: Mv = mu, where M is the weight of rocket with its velocity v and m is the weight of fuel with its velocity u.
Of´course M means M+m1+m2+ … +m9, then M+m1+m2+ … +m8, … , until M.

So we use the maximal speed in the universe, the speed of light. Then there is a possibility to use interplanetary or interstellar matter at a density of, say, 3 hydrogen atoms per cubic centimetre. Especially if we use an extra large funnel that will collect those hydrogen atoms – alias stabilized grouped quantum field excitations into the form of a hydrogen atom. See below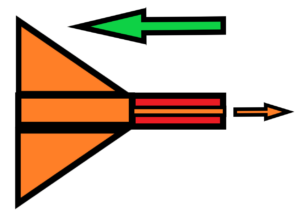 

where the green arrow means the dirextion of the interstellar flight and the orange arrow means the speed c of photons from the accelerated rocket.

There is another criterion – maximum acceleration because of the strength of the material or the strenght of pilots inside that rocket.

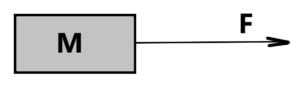
straight movement

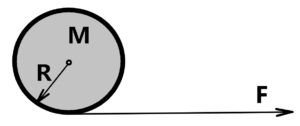
rotational movement

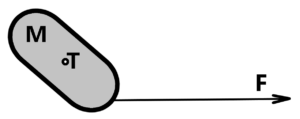
oscillating movement

Try to solve following question – see bellow

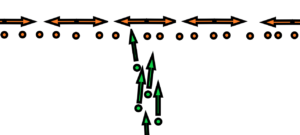
There are N balls. Every of them is oscillating around its zero position with max velocity u without the contact with the next ball. These balls are kept together in the frame with the same distance L. Against these balls are fired projectiles with velocity v. The weight of each ball is M, the weight of each projectile is also M. Collisions can occur when projectiles pass by oscillating balls. Or the diameters d of the balls as well as the projectiles are very, very small relative to the distance L.

The result of the experiment will be a distribution of projectiles on the screen surrounding the whole system in a circle.
The question is – will the distribution of projectiles on the screen change depending on the speed of oscillation of the balls? Respectively, will there be a significant difference in the distribution of projectiles on the screen depending on whether the balls are at rest or in motion?

Very interesting topic – the vault or arch, both in bridges and temples. 

 to be continued next time … 

Steam engines, turbines, pumps, motors, details as valves, propellers etc.