All beauty in the world is not free, but needs boundary conditions – external or internal limitations. See solids, liquids and gases. For all beauty, formative art, craft, science, is expressed in solids, liquids, or gases. The more beautiful, the more gentle.
We have one piece of stone and there can be countless sorts of sculptures in it, but which will be the beautiful, the impressive? How many combinations are there, especially the chaotic combinations, the tasteless and ugly ones. Versus our perception of what is beautiful and impressive.
For our world the following sentence is valid – The more gentleness the more beauties. Quite a interesting event in nature, such incredible gentleness and beauty (see flowers, butterfly wings) is superior to such rough reality. Everywhere in nature we see, we perceive a fine balance that controls the most violent worldly forces – let us call them, for example, the four fundamental forces. Very roughly and violent processes at micro or macrolevel. Microlevel means thermal movements or quantum fluctuations. Macro level mean processes in the universe. See two images below – the left illustrate quantum field and the right illustrate metagalaxies.


In contrast to the immense gentleness about in the middle – see organic compounds, structures and bonds of organisms, especially artworks, musis, craftworks and inventions of human beings. See next image below
The appearence of beauty and functionality in the world – we get a curve of the distribution of beauty in the universe as a function of magnification with a maximum in the middle. And with two minima on each side of the curve. See an image below.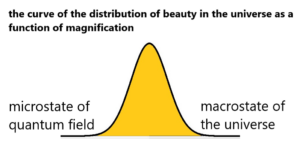
See also artworks. A work of art such as a painting or a sculpture must be viewed at a certain distance. It is difficult to judge details with a microscope or magnifying lens. Or, on the contrary, too be distant. A certain distance is needed, which depends on the size of the artwork. Certainly under a magnifying lens one can see interesting and beautiful details, but under a microscope the interesting and beautiful details will decrease. And when we submit the artwork to structural analysis, that’s the end of the beauty. Conversely, if we move too far away from the artwork, we can perceive the whole, but without the details that give the work its beauty and freshness. And when we move away from the work for tens if not hundreds of metres, we no longer see anything, the beauty has disappeared, our eye can no longer distinguish it. And so it is with the nature around us.
ss. See the ugly disorder of chaos versus the cold and boring beauty of ideally spaced crystals.
It is impossible to derive the meaning of processes of Nature by detailed analysis, or vice versa to consider the meaning of different forms and events in Nature by superficiality. The Nature is like a artwork – there must be details, but these details have to be submitted by the wholliness in proporcional Mutuality. And that’s what exploring Nature is all about, not just works of art or crafts.
See several following images – how to know their purpose, or their beauty, how explain their mutuality in their forms?

What do we see in upper two pictures? First complete chaos and then some sort of order, but strongly chaotic.
The next two images follow – See below

Aha, something’s coming up in a chaotic environment. Some kind of structure. We don’t know what it is, but as we go more and more into the whole, we’ll see. Finally there are the next two images. See below

The more sensitive people can already sense what is going on in the first upper image, the less sensitive ones can see it in the second image above. And then? Next, I’m finished, you can each make up your own imagination.
Go back to the industry:
The machine is not only functional but also beautiful. Beauty is the expression of well-balanced functionality. Functionality not only to the machine, but also to its immediate surroundings. See following image

From observed experience we know that beauty, functionality, and mutual harmony occur in transitional states, areas of transition between pure order and pure chaos. Most beauty is contained in the transition between laminar and turbulent flow. See the beautiful curves when the flow of the medium changes from laminar to turbulent. See an image below
The most beautiful shapes and structures between laminar and turbulent state. This beauty disappears in the chaos of turbulence or in the tightness of orderliness. See the ugly disorder of chaos versus the cold and boring beauty of ideally spaced crystals.
Certainly the chaos, the chaotic appearances are different every time, unexpected and always ugly, disorderly. Certainly orderliness is expected, predictable, but boring and cold, its “beauty” as cold as ice. But transition state – always new, unexpected and beautiful or functional. But when is that moment of creation of transient state? Better expressed, when in space-time appears that impression of beauty, of functionality?
The artwork can only be viewed after it has been made. It is hard to judge the right moment of creation, painting, formation what it will be and how beautiful and stimulating it will be.
True Functionality is connected with Beauty. All the beauties of the world together with the possibilities to form matter are given by atomic physics – more precisely by the intolerance of bound electrons to occupy the same shells in the atomic orbits – see Pauli’s exclusion principle.
The base of matter – atoms. Very stable grouped sets of different excitations of omnipresent quantum field.
- The base of the atom is the nucleus. There must be protons with neutrons together, not only protons. The strong nuclear force Fs makes (attracts) protons and neutrons hold together. It is not really possible to make two protons hold together. There is a repulsion force Fr, then Fr>Fs . See below – protons red, neutrons blue
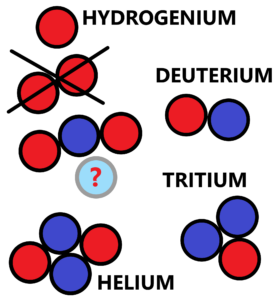
Only one neutron between two protons is not enough. 2*Fs ≅Fr – after decay of neutron, see stability! There must be neutrons, then the strong nuclear forces can balance out the electric repulsion. Then 4*Fs>Fr for two protons with two neutrons (helium) or particle alpha. This fact allows the nuclear fission reaction, especially for the heavier element nuclei. And for the nuclei of the heaviest elements like uranium and plutonium, chain fission reaction is possible. In the other hand to make nuclear fusion is possible for the lightest elements, but not for hydrogen. It is very difficult to give adequate comparisons. Of course, the strong nuclear force is about 100 times stronger than the electromagnetic force. But it has a very short radius with a peculiar trajectory. Moreover, a proton or a neutron are not spheres, but very hard to define appearances of quarks with interchangeable gluons. Just like the electron is not a ball rapidly orbiting an atomic nucleus but a cloud of probabilistic appearance. A wave-particle at the quantum level.
Notice – There is the question of the origin of elements heavier than protons (hydrogen nuclei) at the beginning of the universe. Without a neutron, two protons can’t get close to each other. The neutron is absolutely necessary for nuclear reactions, whether fusion or fission. After all, alpha particles (helium nuclei) are the basis of nuclear physics. The reaction of two protons (hydrogens) fusing together can take place in stars like the Sun. And it’s extremely slow, because neutrons are needed together with a weak nuclear interaction. On Earth, for thermonuclear reactions, we have to use nuclei of heavier elements such as deuterium (an isotope of hydrogen), lithium, etc. Because neutrons are present in these nuclei. When we are on the gentleness and beauty which is expressed on such rough and violent processes (see the stability of atomic nuclei and atoms). It is very interesting how the weak nuclear force by neutron decay controls the strong attractive nuclear force against the strong repulsive electromagnetic force. The weak nuclear force is something like a trigger in a weapon or technological process – a small impulse causes a strong reaction – here the decay of the atomic nucleus.
Let’s go back from nuclear physics to atomic physics. The envelopes (shells or orbitals) of atomic nuclei of the periodic table appear incomplete by electrons, except for the noble gases. The origin of the incompleteness is the electron intolerance formulated by W. Pauli as the exclusion principle. See below part of the periodic table
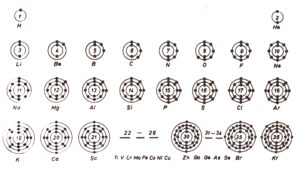
Notice: When we think of electron orbitals, it doesn’t mean some orbits around the atomic nucleus like orbits of planets around the Sun. Electron orbitals mean the probability of an electron appearance in a given space. For the s orbital it is a “spherical” shape, for the p orbital it is cylindrical on both sides, the d orbital is drop-shaped on four sides, etc. The fact of the occupation of atomic orbitals by electrons would be more truthful if instead of occupying individual orbitals by individual electrons we consider their addition to the resulting wave function and the using of orbitals by all electrons together. See the removal of one electron from the so-called highest valence shell results in a change in the behavior of the remaining electron orbitals – their hardening or contracting. I´m leaving out overlaying orbitals in chemical bonds.
Incomplete atoms have a terrific tendency to fill their orbitals to full electron count. This is the origin of the chemical bonding of atoms into myriads of different molecules. Especially carbohydrates. E.g. HF, H2O, H3N (NH3), H4C (CH4), … , (C6H1oO5)n, …
CaF2, … , etc.
The same incompleteness of atoms we can observe in flowers – stamens and pistils, which must be joined by external forces in order to preserve the biological species.
Along with the possible combinations of atoms into molecules, discretization decreases and continuity increases. Such fragile and gentle structures like artworks, like music songs, like flowers, etc, in short such gently structures are modulated at the chemical bonds thanks to the delicacy of the valence electrons placed around such a rough and brutal base as the atomic nucleus is. Comparison – it is the same as with sculpture clay. Such clay has been prepared from rocks by crushing, pulverising and floating it – the result is plasticised fine clay for sculptors and ceramists.
Important notice: the change from quantity to quality is best shown in the chemical elements. The basic building blocks of the elements are three particles – protons, neutrons and electrons. From these three particles we are able to create a huge number of qualitatively different elements and subsequently molecules. The only difference between Helium and Lithium is the number of electrons, protons and neutrons. Similarly, D-glucose differs by a much larger number of electrons along with protons and neutrons in an interestingly ordered set-up – configuration. The more the quantity – number of particles increases the more the quality changes in physical and chemical properties.
This fact reminds me of how so many different things can be built out of sand, cement and water with different functionality that it is unprecedented – blocks, bridges, tiles, houses, pipes, canals, … sculptures, bas-reliefs,… … . Likewise from wood (cellulose) and glue to make a house, a bridge, a deckchair, … …a sculpture, a picture, … , a spoon,… or a plane from the early days of aviation. The infinite possibilities have Cellulose (resp. molecules from H, C, O) in the form of fibres, wood, canvas, glues, … , colours, etc.
See also changes in physical and chemical properties on account of the presence of one added electron (along with the proton and neutron in the atomic nucleus) in atomic orbitals like 1s, 2s, 2p, etc. It is very interesting how a change in the probabilistic appearance of electrons influence the physical and chemical properties of elements.
Let us take a closer look at Mendeleev’s periodic table of elements from the point of view of creation. How many chemical elements are directly mouldable, e.g. in the human hand? Only one: Gallium. Then Selenium ? , … , …then tin, zinc, and copper. In short, tin can be cold-formed, so can zinc, but copper must first be heated to a high temperature and cooled rapidly to make it more ductile.
And that’s the end of it. So we need alloys, like Wood’s metal… bronze, brass, pakfong, etc.
What about wax or paraffin, resin, etc? That brings us to organic chemistry.
But still, clay is the most mouldable. Kaolin, or talc, when mixed with water – it’s beautiful. And after drying, heat it to a high temperature and the shape will stay.
We cannot do without incomplete orbitals of chemical elements. Without which there would be an astonishing amount of other free-forming materials.
Have a look at chemical elements from the point of view – how many elements are in liquid state at 20°C? Only one – Bromine, Br. How many elements are in a gas state at 20°C? Hydrogen, Nitrogen, Oxygen, Fluorine and Chlorine plus (noble gases) Helium, Neon, Argon, Krypton, Xenon, Radon. Summary 11 elements. But only 5 elements (H, N, O, F and Cl) could react with other elements. The rest of elements (more then 100) are in solid state at 20°C.
What does it mean to react? Why noble gases don´t react with other elements? To react means to connect two elements into one subject so-called molecule. Molecule mostly has different properties (melting point, etc) versus the elements of which it is composed.
Compare “nearly” two similar atoms:
C12 – Carbon, there are 6 protons and electrons, the rest are neutrons
N14 – Nitrogen, there are 7 protons and electrons, the rest are neutrons
It´s very strange how very small change makes so big difference in physical and chemical properties. The first element (C) is solid, the second element (N) is gas at the 20°C. Only one electron extra (along with the proton and the neutron) and such a huge change in properties. Which is not the case between Lithium and Beryllium or Boron, where there is also a gradual increase of 1 electron.
See Democritos and his opinion to the origin of matter – there are base elements further indivisible. Such indivisible elements have the same nature (substance), but they differ from each other in shape, size, and weight. In his opinion, air is composed of elements different from the elements of clay, and the elements of clay are different from the elements of water, etc. This means that air, minerals, organisms, wood, water, metals, etc. are all made up of identical elements that differ to each other in shape, size, and mass. And thus also in the mutual arrangement which determines the different properties of e.g. water from air.
We currently understand that all substances in the world are composed of the same elements, three elementary particles (protons, neutrons, and surrounding electrons). These particles form atoms. Atoms differ to each other in mass, size, and shape, This is primarily thanks to the electron shell and a special property of electrons called the exclusion principle. Because of this property of electrons that atoms atomy can be arranged into different groups (molecules). These different groups (molecules) differ greatly to each other in shape, size, and weight. And each molecule has completely different properties even though they have the same basic structure. What’s more, molecules actually consist of a single substance, namely electrons in their indescribable (probabilistic) arrangement around atomic nuclei. Atomic nuclei (roughly written) only determine the mass and number of electrons. But molecules are determined solely by the binding abilities of electrons, resp. outer electron so-called valence electrons.
In short, molecules are differently arranged shapes with different sizes and masses. These molecules have different properties. See citric acid vs. glukose. Both molecules consist from same atoms – C(carbon), H(hydrogen) and O(oxygen). But both molecules have sharp different properties. The glukose is a sweet but the citric acid is acidic. See below

The first image is glukose C6H12O6, the second one is citric acid C6H8O7. We can ignore atomic nuclei when it comes to dimensions. So, the size of a molecule is only determined by the size of electron shells with “connected” valence electron bonds. In other words, the chemical and physical properties (of molecules) of groups of connected atoms are determined solely by their indescribable electron clouds (as with atoms). However, huge number of different possible molecules by the mutual arrangement of several dozen atoms demonstrate such variability in their chemical properties that there is no equivalent among atoms. Such variability reach billions different molecules based on the combination of a few atoms, especially in the case of hydrocarbons. The common basis for this tremendous variability is the electron, or electrons, or rather their mutual incompatibility, where two electrons in the atom cannot be in the same quantum state (have the same 4 quantum numbers). Try to solve, resp. to estimate how many tremendous number is possible by mutual combinations from 83 different atoms (from Hydrogen to Bismuth). Not only hydrocarbons with billions different molecules. But also all possible combinations of Silicone molecules and other metal molecules. Not also these previous molecules, but also all chemical recipes for surface treatment, production of adhesives, sealants, “all” metallic and non-metallic alloys, thermo-mechanical processing of alloys, in short all technological processes in all technical fields – pulp production, papers, construction industry, woodworking industry, horticultural preparations, … , chemical cleaners, … , textile industry including fabric finishing, nuclear industry, optical industry, … , etc. It is not even possible to list here all existing crafts, technical processes and methods. So how many combinations are there using only linseed oil and other additives? Hundreds, maybe hundreds of thousands. Likewise metal finishing, fabric finishing (there are in the order of millions of finishing methods), and to that you have to add thousands to millions more combinations for each technical process. Hydrocarbons and pharmaceuticals are already included, trillions of different molecules. What will be the final number? Trillions of trillions? Probably there are in our world 10E18 different molecules, compounds, mixtures, admixtures, enzymes, catalysts, reagents, yes even dislocations in metallic bonds, etc. This enormous and ever-increasing number depends on one and only one particle called the electron! Resp. on electrons (in principle indistinguishable to each other). So electrons determine what will exist and how it will be stable, what properties it will have. Electrons through its properties They group together and hold atomic nuclei together. Atomic nuclei are subordinate to electrons. Such rough and heavy nuclei are subordinate to such light and indescribable electrons. Atomic nuclei have to do what electrons “demand”—allow themselves to be formed into various structures (molecules).
Democritus was actually right – one particle (the electron) responsible for the creation of a vast number of different forms of matter.
There are the huge number of possible molecules. From very simple molecules like CH4 through more complex like upper mentioned molecules of glukose, etc. until such complex molecules as enzymes, etc. The most complex molecules like enzymes (their 3D models) look like a big lump of clay with no regular shape. See below (3D model of an enzyme made by jstransky)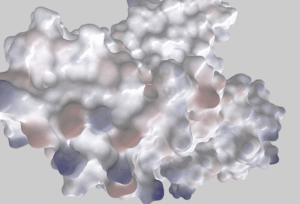
We can see that we can model this at home out of clay, each molecule separately according to the configuration of inner atoms. These different like random shapes are given only by their electron´ valence “cloud”. Finally imagine extreme big “box” of very different molecules grouped together somewhere more somewhere less. All these molecules (different shaped packages of “electron clay”) together and differently perform their “duties” – sugars, building blocks, enzymes, etc. in many organisms.
One molecule (H2O) or two, three … several molecules (H2O) in the closed box. See below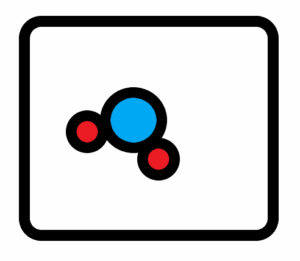
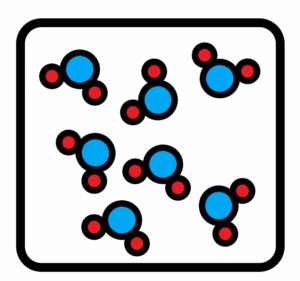
When does the chemical bond start working – the hydrogen bond? Especially in the case – ice, water, steam? When does water start freezing or evaporating? That’s a very peculiar question for one molecule. You always need to have more than one molecule. Only then there is the hydrogen bond among molecule.s And evaporation, a change in state, requires a very large number of molecules. Similarly, the question of when glucose will be sweet or when citric acid will be acidic.
Very beautiful example is the molecule of glukose C6H12O6. Especialy in so familier form of cellulose. If we put the molecule water H2O out from glukose then we obtain molecule of cellulose C6H10O5. But C6H10O5 is not the right, the right is (C6H10O5).n for cellulose. The cellulose is a very peculiar form of matter. It does not dissolve in water thanks to the tight arrangement of hydrogen bonds between the repeating basic parts C6H10O5. The question is, are we able to artificially produce a cellulose molecule from glucose that is so amazingly woven into individual interconnected fibres that, despite its composition, it does not dissolve in water? Notice: pure artificially, without using enzymes.
Go back to properties of base elements like Carbon C, Nitrogen N, Selen Se, Bromine Br, Gold Au and Mercury Hg. Why I have chosen this six elements? Because there is a sharp change in properties among them, despite a minimal change in their electron configuration. The radical change is their melting point. Carbon is a solid at room temperature. Whereas nitrogen is a gas at the same temperature. Similarly, selenium and gold are solids whereas bromine and mercury are liquids. Again at room temperature 20°C.
Here you can see how a tiny, almost invisible change in the microstate can totally change the macrostate e.g. the melting point and other chemical properties. The microstate is the change in minimal quantities at the quantum level (1 electron) between two elements. Macrostate is the significant change, e.g. in the melting point of between two elements.
First, let’s get clear on what temperature is. I’m not going to describe different explanations of temperature based on the “oscillating” speed of atoms, molecules, particles, or spin systems. For this example, let’s just say temperature is how fast atoms oscillate. The faster and more intense the “oscillations”, the higher the temperature.
However, temperature in itself is meaningless. There have to be limits. Without limits there is no oscillation. Oscillating atoms must be in a closed (limited) space. And the closed space cannot be created without solid substances, in the case of electrically neutral atoms. Thermally “oscillating” atoms can also be ‘enclosed’ by a strong gravitational field of a body such as the Earth or other suitable celestial bodies. Here, the gravitational field acts as a ‘limiter’. Imagine gas in vacuum (interstellar) – there is impossible to “oscillate” resp. to bounce between each other or between limits (boundaries).
… to be continued
What’s the point of all this? All the “incomplete” atomic orbitals, all the samples whatever there are in nature. What is the purpose of knowledge whose current state is the quantum field theory – field properties of matter and radiation. The “peak” is the wave equation starting with Erwin Schrödinger. There is a new base unit – Planck constant as a speed of light. How to prove, how to verify that Planck’s constant is always the same throughout the history of the universe? After all, in physics we measure only and only ratios – the ratio of the measured quantity to the base unit. How do you detect a change in the base unit? Yes, in terms of the basis of knowledge, there have been no new discoveries, no new fundamental insights. It’s still just a reworking of the procedures for solving the wave equation and applying it to other systems and problems – certainly quantum computers, certainly the discovery of gravitons, quantum chemistry and many many more. But basically it is just a confirmation of physics ideas that are 70 years old and more – gravitons, antimatter, quantum fields with zero vacuum fluctuations – with excited particle-waves that repeatedly disappear and appear again. It is still just a reworking of the wave equation solution procedures and its application to other systems and problems, still just a calculation of quantum states, e.g., standing wave states associated with particle-waves. What is remaining? A unified field theory? Reducing quantum mechanics to the simple statistical appearance of particles, impulses and energies is hardly possible anymore. What then? To find a universally valid formula for ever-changing conditions? Reality still surprises us, it is impossible to write a universal formula. A universal formula for chaotic events or a universal classification of biological species. However, the difference between the biology of the Palaeozoic and the current Quaternary is fatal. The answer is probably for each person to decide for himself in what situation he finds himself.
E.g. Imagine a botanist who describes the Devonian flora with all its peculiarities – a very rich and beautiful Devonian flora. He will recognize and name the basic botanical species, then group these species into superordinate units – kingdoms, etc. At the same time, he then finds that no two botanical species are identical. Thus it finds subspecies, etc. Imagine some “miracle” and the botanist is transported to present time – he can start again – there is an immense difference between today’s and Devonian flora. Our botanist will again have to identify the differences, to name them, to look for connections, common characteristics, etc. And when it’s all done again then botanist will move forward in future about 100,000 years. Flora changes over and over again into new unexpected forms and our botanist will have to identify, to name, to classify and start again and so on ad infinitum. He’ll probably get tired after some “trips” through the time. But at the same time, almost every gardener would give an answer to our botanist. The gardener can plant new roses, previously unseen shapes and beautiful combinations of flowers. This gardener is certainly not bored – there is always something to improve, to combine, to increase the resistance of different kinds of plants to different and changing conditions. One could even write – that this gardener will be happy, and happy forever. Likewise an engineer designing new machines or an artist creating new works together with a craftsman.
It is the same for all scientific disciplines, to describe, explain, generalize and predict – this is certainly correct, but the validity of all theories (verifiable in practice) is limited by its very nature – abstraction, i.e. generalization based on the recognition of what is important and what is not, what can be neglected and what should be considered. And no one can predict for a long time what will happen when previously negligible events become important and vice versa.
Not to mix reality, real processes, forms and events with the description of their state in the forms of theories and laws that follows from it. Law, laws, theories are invented (derived, constructed) by people on the basis of abstracted real processes in a given time and space.
By the way – see quantum mechanics in prehistoric ages. Especially metal treatment by thermal process. The ancients found it very strange when they heated a metal it would first not shine, then appear dark red, then red, then orange to yellow colour and finally almost white. However, the colour of the radiation should have been the same – only changing in intensity from the slightest shining to a blinding shining. It is very strange to change colours!
Imagine a few person through the history who want to understand this mystery. One of the interested ones takes the help of a glass prism, which separates the white light into its individual colour parts in a spectrum. So let’s imagine a simple experiment – a heated black iron body (the flames go completely out, only the black body is visible), then a thermometer and a prism, a shade in a darkened room and an observer. What will he see? At low temperatures of up to a few hundred degrees Celsius, nothing (no spectrum or coloured parts of it). Above 500°C, he will see a dark red colouration, the intensity of which will increase as the temperature rises. At over 600°C, the observer will see a bright red light that seems to come out (it is suspected) and suddenly ” jumps out” at a certain temperature. This catches his attention and he writes down the temperature. As the temperature of the body is increased, the bright red glow becomes much more intense and at temperatures above 700°C it is as if the yellow component in the orange can be seen and suddenly the observer sees a bright orange component along with the bright red component along with the yellow component that has clearly jumped out of the spectrum. And again the process repeats itself, the temperature increases and only the intensity of the mentioned colour components increases. And at temperatures above 900°C, the green-blue component is revealed along with the blue component, with a subsequent ” jumping out ” of the blue part of the spectrum. The temperature now rises above 1 100°C and we have the violet component already visible. i.e. the inner observer in a darkened room sees the whole continuous spectrum.![]()
Whereas the outside observer who heats the iron body only sees colours from dark red, through red, orange, yellow, yellow-white to bright white with a blue-tint at a temperature above 1 300°C and the iron burns-wastes.
The “jumps” are not to be taken as sharp jumps, but as short temperature intervals when another colour appears. These short intervals are short relative to the long temperature intervals, when only the intensity of actual colours increases.
It is clear that the intensity of the radiation increases proportionally with increasing temperature, but the frequency of the emitted radiation increases in “jumps” as a function of increasing temperature.
It is possible to make upper mentioned experiment preciously – to prepare suitable black body heated by electric power. The mass of such body is known, e.g. a platinum, then we know the number of atoms inside that by using Avogadro const. The we use so accurate thermometers and very good prism with scale on the visor. We know the thermal energy of 1 atom – E = m*c*dT where m is the mass of the black body, c is thermal capacity of this body and dT is difference in absolute temperature. In this way we can detect with more or less accuracy the temperature “points” where the frequency of the emitted radiation changes rapidly.
… to be continued
Notice: Not only electrons in atomic orbitals are quantized, but also our perception of colours.
A short note on the origin of waves, particles, atoms, chemical bonds and thus molecules. Let’s have an ice crystal. When we heat this crystal, we get water or water vapor. And when we cool the water, we get the original ice crystal again. That sounds logical. We even know why it happens – chemical bonds dependent on internal energy. But let’s think differently – at the beginning of the universe, according to known hypotheses, there were no ice-snowflake crystals. Where were hidden the laws of physics in promordial forms of our universe? Where have the kinds of chemical bonds (exclusion principle for electrons) been hidden? Where was hidden the diversity of chemical compounds and the diversity of biological species through geological epochs? Let’s go back to our ice crystal. Sometimes in the primordial forms of our universe the “condensation” of particle-waves must have started, then the fusion of atoms, but according to what laws? Where have all the laws been hidden? However, laws, rules and processes are frameworks – each species is an unrepeatable original – no two snowflakes in the world are exactly alike. Every physical process is slightly different at the quantum level. What have been the degrees of freedom in the beginning of the universe? In other words, what was randomly realized in a given framework, what “condensed” in the course of the cooling of the universe, already has a uniquely given path with all the reciprocal properties. That leads to the framework repeatability of physical and chemical processes as we know them today. If we accept this hypothesis then there may be other groupings, other chemical bonds and other biological species in different universes. The temporary conclusion is – random processes take place in a given frame and these are then repeated, again randomly, but in a sequence of given frames, which frames then gradually change. Randomness vs. necessity. But there is a contradiction. If the particles are roughly the same (or so we think), why do biological species change rapidly over geological epochs?
If we plant a pine seed it won’t grow into a maple tree and vice versa. This is the way the world works. Although pine trees were not in Devon and in the future… ?
Similarly, zinc sulphate does not crystallise from a solution of dissolved sodium chloride salt. And in the very beginning of our universe, sodium chloride could not have been thought of as being in such beautiful cubic crystals.
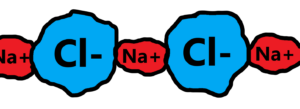
See different crystalls of different chemical elements and their molecules – how they can hold together such chaotic structures in such beautiful forms of crystal structures. E.g. crystall of NaCl – its cubic lattice, see below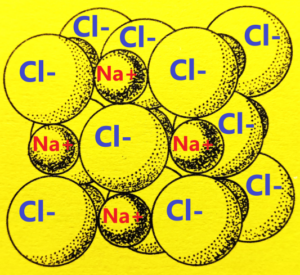
For NaCl molecules, the situation is clear, they are connected by the valence electron of sodium, which is taken up by chlorine. But what about the crystal, you can’t think of molecules there. Actually, a NaCl crystal is roughly one big molecule. How can two negatively charged chlorine ions be kept together? It is impossible – they’ll repel each other. See below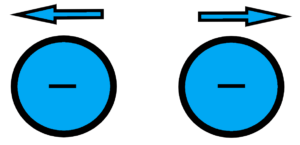
How to keep them together? Only to put a positively charged sodium ion between them. See below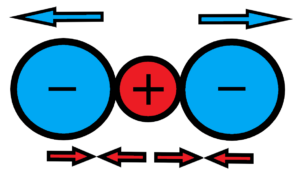
The attractive force between the sodium cation and the chloride anion will be greater than the repulsive force between the negatively charged chloride anions. It’s a bit like an atomic nucleus, how to hold together positive protons, just put neutrons between them to introduce a strong nuclear bond. After all, protons and neutrons as elementary particles are only formed and renewed chaos in the “ocean” of the matter (quantum) field and their appearance is far from being as spherically ideal as the pretty pictures necessary for mathematical models. And it is the same with the atoms of the chemical elements. See below – it may be distorted, but this is more about reality
However, atoms as well as elementary particles are ever-changing irregularly bounded forms of matter field excitations. And that’s not counting the thermal oscillations of atoms and molecules.
The crystall of NaCl – its cubic lattice – see below
It is very interesting how the above lattice holds together, especially if it repeats many times up to the size of a visible salt crystal. But such a crystal, quite neatly cubic, is rarely found. It takes a lot of work and effort to create the optimum conditions for crystallization of pretty cubic salt crystals larger than a few mm.
There are two extremities something and nothing. See black filled space of limed size and white filled space of the same limited size. See below
If the two spaces are joined into one space, the blending will lead to the final balance at the level of grey, grey colour. The saturation of the grey fill will depend on the initial black to white ratio. See below
It is possible to write that the disorder of space has increased, thus entropy has increased.
… to be continued
Go back to the Beauty and Functionality in the world. Where was an artwork (in the same way every product) before it was created? In the beginning there was a movement of Wisdom (mind) inside the creative man, after that there was the artwork. What’s going to happen to the artwork through its entire existence? What happens to the artwork when it ceases out of existence? There will be new artwork better then last one. But creation ability is not possible to destroy.
Some people are so sensitive to feel hidden intention which will then be seen visibly in the world. The purpose of our life is to grow in this experience to perceive the invisible hidden intentions by verifying this perception in its visible results in the world. More about it in section Theology.
See abstract images and real images. Not only artworks but also pieces of engineering endeavours such as machinery, engines, clocks, turbines, etc. We are familiar with real images or real engines. Abstract ones are new to us. But like real images then abstract images could be beautifull. Their common attribute is a beauty. In the first case – the beauty in the real world, in the second case – the hidden beauty gradually becomes visible. It’s the same in engineering. The common attribute is a functionality. Real images for us could be abstract for others and vice versa. Consider the prehistoric fauna and flora of devon could be abstract for us. It´s the same in engineering – consider the first engines in the 19th century.
Current nature in the world with real images is only one expression of Beauty. One expression from many possible expressions, from infinity possible expressions. The common denominator of all images („real“ and „abstract“) is Beauty at any kind – shapes vs. colours. See also multiverse universes.
Engineering – interesting development of human beings called engineers. In the beginning, in prehistoric times, there was only ore, coal, limestone and fire. Throughout ancient times, engineers made metal tools, weapons and simple mechanisms (water wheels, screw pumps). In the Middle Ages, engineers built he first mechanisms such as mechanical clocks, weaving looms and so on. Not that mechanisms built or replicated themselves. And in modern times, we already have mechanical computing devices, typewriters, precise pendulum clocks, right down to high-precision atomic clocks.
All tools, devices, devices over the ages (from swords and knives to various mechanisms and processes to high-precision atomic clocks) did not happen randomly. They didn’t just happen by the way. But they were created by a big effort, a painful experience of a few people called engineers. The painful experience was replaced by the immense joy of a working invention or of putting an idea into practice. It doesn’t matter what you are, if you’re an engineer, scientist, artist, craftsman, carrier, economist, hairdresser, pilot, doctor, teacher or something else. One should be something – to reach the fullness of humanity. Live out the painful experience with following immense joy of the obtained abilities. And so still. In engineering, there is no absolute best solution to a given problem. There is a good solution and an even better solution. But no one can guarantee that the even better solution is the best.
The devices were built not by themselves, but by experienced and capable people. Watchmaking is a beautiful example. The accuracy of clocks increased through the ages to the current level of atomic clocks. These instruments did not self-construct, they were built by engineers. In fact, the machine with given accuracy produces another machine (even itself) with a given original accuracy – no more! A machine production with a given accuracy cannot produce, for example, more accuracy gears than the given accuracy of the machine.
At first glance, a mystery of increasing accuracy of products. How to achieve with a given accuracy of the production machines a much higher accuracy of next products?
Emission of photons from atoms – jump electrons to a lower level. See line spectrum. The line spectrum is not an ideal line, but a probabilistic distribution of radiated frequencies with a peak in the middle.
All frequencies are close together in a given probabilistic distribution. It can be assumed that each frequency is unique, unrepeatable. For the reason we know that we can insert an infinity of other numbers into the smallest interval on a number axis. Even each radiated frequency could be expressed by an irrational number – see the square root of two, or five, etc.
The defined difference df in radiated frequencies is not a fixed value, but a value changed in a given probability distribution. The same is valid for Planck´ constant.
See steam enegines, or Stirling engine or Otto engine or other types of thermal engines (combustion enegines, turbines, etc.)
There have to be two chaotical environment which differ to each other. And then, only then, a gradient or flow from the environment with higher intensity of collisions to the environment with lower intensity of collisions is created. The flow, although chaotic, is more or less coherent with a dominant direction. Which means that the ever-present chaotic movement is subordinate to the general direction of flow.
See clocks, mechanical clocks or crystall clocks, etc. Periodicity is the key. Whether the frequency of electromagnetic radiation or the number of oscillations of the pendulum. The result of the measurement of time is the number of the oscillations made around the equilibrium position. To satisfy the above, we must have an equilibrium position and the deviations from it. This is nicely satisfied by thermal fluctuations. But the question is how to count them and, more importantly, whether their oscillations are regular. And so we have pendulums, or flywheels, or an oscillating quartz crystal, or the oscillations of a maser. The last source of “regular” oscillations is thought to be more accurate.
E.g. a mechanical pendulum clock – we need a pendulum, a planet or moon (or at least an accelerating rocket), an initial impulse, and that’s it.
to be continued …
to download following files
| Download | Download | Download | Download |
| Technical drawings | |||
