Where base units come from and how they are related to each other? The second, the metre and other base units are useful approximations for describing our universe. What we measure are mere ratios between measured values and base units. The fundamental question is how to measure the dimensions of spacetime with utmost precision if every part of the universe is constantly changing, and not only due to the thermal motion of atoms or molecules, but also quantum vacuum fluctuations, not to mention the expansion of the universe.
See – Base_units_preview
All base units are referenced to time. What is time? Rather, let us ask, how do we measure time? We certainly don’t measure time by chaotic changes, random changes, or changes in transition states between chaos and order. To measure time we need regular changes. When did time begin to exist and when does it no longer exist? The measurement of Time exists only and only because of regular changes. Thanks to changes that we consider regular – such as the various oscillations, starting with the pendulum, then through the quartz, and finally through the oscillations of electromagnetic radiation.
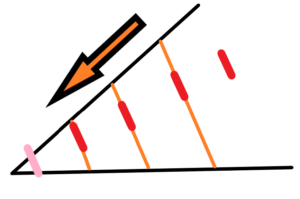
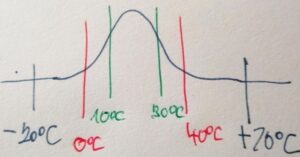
Let’s have the progression of a mathematically indescribable function. There are different parts of the function. And some parts appear to be regular oscillations. – see below

In the upper image we can see the parts where time can be measured. And then we see the areas where it cannot be measured – we do not have a reference regular process, in our opinion. Or how to verify the regularity of the pendulum oscillations? By an electronic quartz clock? How to verify the regularity of the oscillations of a quartz clock? By electromagnetic radiation from a maser? How do we verify the regularity of the oscillations of ELMG radiation from a maser? …… ? So we assume that the ELMG oscillations are regular.
Imagine the world without regular stabilized events, e.g. so called oscillations. Imagine the world where are no constant rulers like a meter or yardstick. Such world seems like a garden where are no fixed rulers. How and by what to measure inside this environment? There are no regular stabilized grouped events like oscillations, or yardsticks, no fixed shapes.
Imagine a garden or a landscape where we came or were born. Everything is changing, more or less. We need to measure the area of the future planting bed. What to use as a unit of measurement? We use something that hardly changes. Like an oblong, solid stone. That’s the unit of length. Then we just take a rope, mark the length of the stone repeatedly on it and we have a ruler. We can have more ropes (rulers) and check them occasionally with a basic unit of length. Let us not forget that our basic unit of length is taken from the garden, the more or less variable garden. We have no basic unit from anywhere outside the garden.
It would be a very unpleasant situation if everything was changing, in short, even the “stones” were changing like plants. Our measurement of the area would not last long – or would only be current for a very limited time:-)
But fortunately we have a stone that at first sight is indifferent to all other changes. But as time goes on, we find that even the stone is somehow smaller, perhaps by the decreasing pattern on the surface of the stone. What to do? What to do? We won’t give up and we’ll see what the stone is made of. So we’ll break the stone, another one, not our base unit. Then we find that the stone is made up of indivisible particles. These indivisible particles change rapidly and unpredictably within a given tolerance, e.g. plus or minus half a particle. And when we take a closer look at everything in the garden, we find that everything is made up of indivisible, rapidly changing particles – the flowers, the soil, the air and even our observing instruments such as a magnifying glass or a microscope. And it can be supposed that we, as observers, are also made up of indivisible but rapidly changing particles.
We need “regular” and “stabilized” grouped events (units) for our abstraction – to recognize shapes, structures, objects and processes, to name them, to count them, to predict them, etc. We use these units to measure other shapes or structures that change. But beware, we are defining peaks of stabilized grouped events. We use them to measure other peaks of grouped events. It is difficult to suppose that these peaks will not change in accordance with the surrounding fluctuations. These grouped chaotic events can be describe mathematically. To put the peaks of their appearances apart and numerate them. Actual peaks of probabilistic distribution of appearance of excitations grouped together, respectivelly solved (mostly average) peaks represents the number for distance, time, temperature, intensity, etc. It doesn’t have to be like this all the time. Such changes there are a big source for potential big deviations. See butterfly wing effect – the waving of a butterfly wing causes a chain of events on the other side of the Earth. But there are hundreds and hundreds of trillions of wing movements in the chaotic fluctuations – and the question is what gets cancelled out, what gets amplified and what stays as background noise.
We can take base units only from our space, from our universe. There are hardly any external units of measurement. External units from outside our universe. As in the case of the measurement of the expanding balloon or circle or the extension of the heated rod. In these cases we have external meters. But if the unit is part (scratches) of the heated rod or the balloon or the circle, what do we measure? Will there be any change? Certainly, not. The unit (scratches) is also changed by heating or by inflation etc.
Consider an experiment – Let´s measure the difference in length of a long steel rod as a result of thermal expansion. Connect a steel ruler on cold steel rod and you have a starting value. Heat the rod and again connect the ruler and we get a different, higher value. The heated rod has elongated. But if I keep the ruler on the rod for a long time, the difference disappears.
Not to mentions, the scale is good for normal comparisons, but dividing 1 m (alloy) by one million or even a larger number is a question mark, because we do not know the effects at such small levels relative to the alloy of the meter. Now we have the number of electromagnetic oscillations as a measure of the meter. That’s good – the accuracy is increasing rapidly. But again, to divide one oscillation by one million or even a larger number – again, a question mark, see above. Thus Planck time, a number so small relative to one oscillation of the atomic clock.
How does light travel such a small distance in a vacuum as the Planck length? Do we know anything about it? Do we suppose continuously and smoothly? Well, the vacuum isn’t that continuous and smooth.
Imagine the next situation – see Figures below


There are several „regular“ shapes – blue or white circles. See their nearly regular appearance and their nearly regular distance among them. How to choose a base unit among them? For small areas we can take distance and size among circles as almost regular. If we look closely, they are not regular. How is possible to explore this? With a help of the choosen base unit, that is irregular as everything arround? There is no absolute unit no outside ruler, only ratios among the selected base value and the measured values. See the image below – there are biological growing plant cells

These plant cells are separated from germ cells by their dividing. Then these cells are growing like our spacetime. But we are inside these cells. And we can´t use any external rulers. We can use only internal rulers like the size of cell or its part.
Our universe is like an elephant. Try to measure a growing elephant. From baby elephant to adult. I don’t mean measuring the elephant with an external ruler, but an internal ruler derived from the elephant.
What do we choose as the base unit of distance? Probably something clear, clearly defined, like a bone or a vertebrae. And as the elephant grows, the relative sizes of the elephant will change. But our basic unit will also grow. We cannot find in the elephant, as in the universe, a fixed, reference point or distance.
In the future, instead of the cesium atomic clock, the base unit of frequency (time) could be replaced by frequency of the relict radiation. The advantage of this radiation is its omnipresence in the universe and its homogeneity. The wavelength of the relict radiation is approximately 1 mm. Thus, it is usable for our instruments. The “biggest advantage” is that the universe will stop “ageing and cooling”.
E.g. speed of light in vacuum – 299 792 458 m/s (meter per second)
From system of base unit SI we have a definition for one second 9,192,631,770 periods of radiations of Cs 133 (atomic clock)
1 meter is defined as a is the distance travelled by light in vacuum for exactly 1/299792458 of a second
add the definitional values to the expression for the speed of light
1 s = 9 192 631 770
1 m = 30,663 319 = 1/299792458 * 9 192 631 770
299 792 458 m/s = 299 792 458 * 30, 663 319/9 192 631 770 = 9 192 631 770/9 192 631 77 = 1
the speed of light in vacuum is exactly 1
One of what? Well, just one. In the same way, we find that the mass of a hydrogen atom is approx. equal to the mass of a hydrogen atom, or a carbon atom weighs approximately as a carbon atom. Nothing more, nothing less.
Next example – we have the space that is expanding – two lines intersecting at one point at an angle 30° – inside this space there are expanding lines and next 2D objects – this space expands next to us – on paper, for example, and we have to measure the speed of expansion, etc See the Fig. below
There is a crucial difference between the view from the inside and the view from the outside. When did the 2D space begin to exist? If we are outside of the expanding 2D space then there is no problem. But if we are inside … ?
Let’s imagine two-dimensional beings who live in a 2D dimension and want to know the speed of the expanding of their 2D space. These 2D beings will do as we do, choose units of time and distance (red marked) and determine the center – where all expanding objects converge (from their observation). But their units of time and distance are internal part of the expanding 2D space. so they will expand too, partially (bound mass) or completely. Here the situation is much more complicated. 2D beings do not have an external coordinate system independent of the expansion of their spatial circle. It is hard to believe that near the origin the unit of distance remains constant even though it may otherwise be stabilized during next expansion (pink marked).
From our 3D view outside their expanding space, we can see how their unit of distance also changes. Inner base unit of distance from the outside view will decrease towards the centre of expansion and vice versa the size of the base unit will increase with growing distance from the centre of expansion. For this reason, 2D entities measure a much larger distance of their space. What’s more, if they go more to the center of their circle, they will never get to zero – it is an ever decreasing infinite series of units. Not to mention the basic issues around the definition of distance and time. When did time begin to exist? Time began to exist along with matter – with objects that have a speed of motion significantly less than 1 – the speed of light. With objects where there is a slippage between time and distance. With objects that have a non-zero rest mass as opposed to photons.
The same problem will be with determining absolute motion, absolute temperature, and other “absolute” values inside an ever-changing space where, of course, relative proportions are valid and where it is possible to determine very well what is about to happen. See internal combustion engines, airplanes, nuclear reactions and much much more. What we have learned in a given limits, e.g. about nuclear reaction, we are able to repeat it succesfully at any time and anywhere in given limits in the world.
See the parable from botany – the basis of the distance unit is the plant, virtually clearly identifiable distance between two of its leaves. Why not use this measure for the current state and for the more or less recent past or future. But using the previously mentioned unit to solve for the early stages of a plant’s development or even its embryo – that is, rather irresponsible.
As can be seen from the previous examples – the validity of base units, as well as the validity of all comparative measurements, is limited to a certain range – within the given limits where we know the properties of natural processes. And we are able to measure them, repeat or otherwise analyze them and thus predict them.
E.g.: take the size of quantum fluctuations as the base unit. That’s not possible. For these are always changing, they are always different, but still equally chaotic. See the untuned TV screen – chaotic fluctuations. So we have to use a tuned TV screen with a TV program on it. How do we choose the base unit on the TV screen? There is only one requirement – the existence of a TV program! Only in it we can look for base units – time or length or other. We have to watch the TV program carefully. The unit should be regular, or rather should appear regular to us – for example, the change in the height of the sun above the horizon (sunrise, culmination, sunset). After a while we find that we need a more precise measurement. Thus, for a precise measurement, we choose the wavelength of light. Over time, through precise measurement, we find that both the wavelength of light and all the objects and processes in the TV program on the screen are influenced by chaotic fluctuations. In other words, processes that we used to think of as regular are not so regular. The effect of chaotic fluctuations is very small for a regular TV scene. But at the micro level, the effect of chaotic fluctuations is fatal – see the wavelength of light as a base unit.
Precision measurement of the energy value at the atomic level can only be made at the cost of losing information about the duration of the measured energy. In short, we know the measured energy, but we do not know the duration of the measured energy. And vice versa. If we know the time, we do not know the value of the energy. Another result of Heisenberg’s uncertainty principle.
Energy, and therefore matter, is the source of gravity and affects gravity. Bound energy (matter) exists in certain sizes, packages – in short, in quanta. Free energy (matter) can be freely continuous, divisible. There are no quantum frequencies. The frequency of a free electron can be any value as opposed to the frequency of a bound electron.
Bound matter (bound energy) is a quantum system. This is the source of quantum gravity. Just as free energy (matter) is the source of gravity. There is a fundamental difference between bound and free energy. And that is in its action. For the action of the gravitational field, see general relativity.
Relativity is subordinate to the quantum system and the quantum system is subordinate to relativity. There is an interaction between them.
What can I say? That the system of measurement, the system of base units, is limited both from above and below. And it is not possible to freely divide base unit and other physical values into many levels without knowing the properties of the natural processes at the relevant level.
The basic problem – the expanding universe versus base units. The universe is filled with matter and radiation. Matter and energy have the same basis – quantum fields. Both matter and particles are excitations of the quantum field. Basically, there is not that much difference between radiation particles (photons) and matter particles (quarks, protons, etc). Both are material, both carry energy and have mass, and both are wave and particle in nature. With matter, particles are always just slower than their waves, and a lot of the “motion” here is hidden in untranslated forms. Whereas with radiation, the particles (photons) are as fast as their waves – all the energy is “free”. This is why matter is sometimes described as frozen or bound energy. See images below – there are two basic models of our universe. Matter as particles – marked with circles with different size. The question is whether particles change or are stable during the cosmic expansion. And whether we’re able to find that out. Find out using internal units.
There are two basic models of our universe. The first model with a beginning and an end point, here the universe expands and then contracts. The second model with a beginning point (it may not be a point, but that’s later) from which the universe expands to the big rip.
Both models have one thing in common – the base units are chosen from the universe itself. Base units are internal and not external. The universe changes (it may change in other ways than the above two models) and so do the base units. Do particles expand like radiation ? (see relict radiation versus the whole spectrum of electromagnetic radiation). Anyway, base units for time, distance and others are derived from our universe. We don´t have outer base units for distance and time. No outer ruler. No outer oscillations. We have only inner rulers, inner oscillations. We have chosen one of oscillations as the basic one for others. See the definition of time based on the cesium atomic clock – 1 sec. is nearly 9 bil. oscillations.
It is possible to plot a triangle on a spherical (or other) surface to determine the degree of curvature of the space. But only if the gravitational field is uniformly distributed on the spherical (or different) surface. The ruler remains the same, although curved (which we cannot detect), but the distance between the lines of the ruler is constant. If the gravitational field is inhomogeneous, then in a given part of the spherical (or different) surface there will be not only a change in the curvature of the ruler, but also a change in the distance between the lines of the ruler – which of course we cannot detect. We are inside and not outside with rulers.
The basic question is – do the basic units change in accordance with the expansion of the universe? Or are there stable basic units like the “good old” platinum-iridium alloy that seems not to be expanding. Or is there a slippage in matter between expansion of the universe and a change of e.g. the length of a material object like the alloy meter above.
Consider an elastic membrane, a rubber sheet in the shape of a circle. We stretch this rubber sheet equally on all sides. Let’s put different shapes on the sheet. Waveforms of oscillations, for example. It’s clear that the wavelength of the oscillations will increase as the sheet stretches. But relative to what? Where is the reference point? Relative to us, the observers outside the elastic rubber sheet. Imagine that a two-dimensional sheet is populated by two-dimensional creatures that know only two length dimensions and time. These do not measure any change as the sheet stretches. For their bodies are an indivisible part of the sheet, hence they also stretch, including their scales. See images images below.
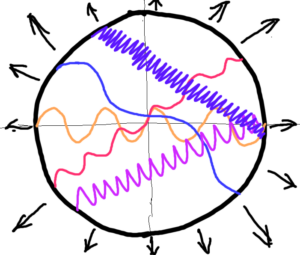
Let us go further – stretch or contract the stretched elastic rubber sheet locally at several points (points) A, B, C. This gives us local changes in curvature. Creatures inhabiting the sheet are able to measure these local changes of curvature. However, this has one requirement, creatures must be outside the local curvature changes. Their reference point is outside the measured local change in curvature. Then creatures will measure a wavelength´s difference. The difference between the etalon (oscillation) and the measured oscillation at the local change of the point A. The etalon is the wavelength of the cesium atomic clock – all integral to the whole elastic sheet. That is all. We do not and cannot know the wavelength of the etalon of oscillation. It is one. One of what and relative to what? To itself. We can only measure differences between the oscillation etalon and the measured oscillations.
But an outside observer ( the three-dimensional human beeing) can measure how big the etalon wavelength is. He can also measure how much the wavelength changes as the sheet stretches. But even this external observer is limited by his three-dimensional expanding universe. His cesium atomic clocks do not allow us to determine their absolute length or duration – we only know that 1 sec. is approximately equal to 9 billion oscillations. So there may be another observer above the universe, but even he will be limited by his superuniverse. And so on ad infinitum. A kind of relativity of distance to infinity. It’s reminiscent of Cantor’s exponential sets of infinite sets or Gödel’s theorem on completeness and contradiction-free axiomatic systems.
Let´s go back to the reality of an expanding universe with everything that is part of it – including observers, nature and the measuring instruments.
Imagine a flat space only with two dimensions that expands (see images below) two-dimensional space filled with adaptive quantum foam – all three images show us the expansion of the universe – a hyperbola, a circle or another shape that can change. Is it possible to detect this? By using measurement methods that are internal parts of such a universe?
inside the flat space, the base unit of length – the ruler – is selected (two thick lines). There are two choices for selecting the ruler. Firstly, the ruler changes in accordance with the expansion of the flat space, which is filled by the adaptive quantum foam (black thick line on the left). The second case is different – here the quantum foam is bound into stable structures. The ruler is selected from these structures (gray thick line on the right). In this case, there may be a situation that the ruler remains the same during the expansion for a certain period of time. We do not mention the question of the emergence (disappearance) of bound forms of quantum foam in the early (end) stage of expansion.
How to find out the expansion of the universe? Not to mention that the universe could expand differently in different places.
How to measure the density of an omnipresent ocean of quantum vacuum fluctuations? Not only can we not directly see the fluctuating quantum field (only indirective evidence) – the so-called zero vacuum fluctuations, but we also cannot know what the density of the quantum fluctuations is. And whether the density of the fluctuating environment changes or remains constant. For example, it is a difference in the maximum speed in the universe – the speed of light. We have hypotheses that propose to measure the relative velocity between high energy gamma radiation versus low energy radiation (UV, light, infrared). Gamma radiation should be slower velocity than UV radiation because of the quantum nature of the ” support” medium (quantum foam). Just as in everyday life, a car with larger wheels will go faster (relative to the roughness of the road) than a car with smaller wheels that “copy” the roughness of the road. Both wheels have the same circumferential speed, the small wheel turns much faster than the big wheel, but the small wheel has to copy the rough ( lumpy) surface of the road (up and down). This is not a rejection of special relativity, but a confirmation of it. Theory of relativity is exactly valid in flat spacetime without metric defects. That is, an ideal circumstances that does not exist in the universe. Just like an ideal point, an ideal line in mathematics or an ideal gas in thermodynamics. In other words – in an equally “dense” quantum field, light will travel equally depending on its wavelength. Not to mention possible changes in the “density” of the quantum field. This cannot be verified by our units of measurement, but neither can it be negated.
What is the age of our expanding universe? Measured by the universe itself? Measured by the rulers (oscillations) that result from the properties of the universe? The basis of science is a unit of measurement – one distance (number of oscillations). Probably such unit is changing over time. How to estimate the past or the future, especially what was before the creation (selection) of the unit?
It’s impossible to measure time near a singularity, close to zero. We don’t know the nature of the events near our calculated absolute zero. It is impossible to reach 0 K in the same way as to reach 0 sec. Especially with derived units from something, not from nothing. The measuring frequency-ruler has a period. Near the singularity, this period would be higher and so the frequency increases. In other words, there is a change of ruler.
We are trapped with base units or base rulers. They’re just relative not absolute. We are able to measure e.g. a prolongation of thermal expansion of a steel. Such measurement is provided by external ruler independent to prolongated steel. How to measure the prolongation of the steel by inner ruler?
See the expansion of our universe. There are three possible processes:
– units or rulers do not change, they are stable despite ambient changes
– units or rulers change in accordance with the expansion of our universe
– units or rulers slightly change (slipping) in relation to the expansion of our universe
We suppose rulers do not change in relation to galaxies moving away to each other. But it’s hard to believe that there are “fixed points” inside the universe that keep their proportions despite all the changes, especially when everything is made up of those “fixed points” – atoms, molecules, etc.
Let’s go back to the question that occasionally occupies our minds. What’s going on in Pleiades (e.g. near Electra or Maia) now – right now of our earthly time. This query is meaningless. Anyway, there’s no point what’s happening in one place of the Pleiades now, right now, think in our earthly time. Every part of our universe has its own time – there is no coincidence. Same meaningless query as what is the absolute value of frequency 1 oscillation. What an absolute size? We cannot know or measure the absolute size of one oscillation. We have no external rulers. We are able to measure only and only the ratio of one oscillation to another or more oscillations. We can select one oscillation as base unit for others and thus compare (measure) not only the oscillations, but also all irregular happenings in the world.
An overview of the basic unit definitions shows the following:
the basic unit of the base units is time – the definition of time, then we get the base unit of length and mass.
Roughly written — we can reduce all units to frequency — the frequency determines the time, length, and mass. The higher the frequency, the higher the mass. The same is valid for temperature – or thermal movement of atoms or molecules. But it’s not so clear here. Heat energy versus temperature. Thermal energy is given by mass, thermal capacity and temperature. The biggest problem is the thermal capacity, which is difficult to define, and if so in a small range of temperatures. The reason is the internal bonds in molecules. After that the properties of atoms – chemical elements and in the end the excitations of quantum field.
The hypothesis about expansion of our universe is supported by many experimental facts. But this hypothetical universe is the result of abstraction just like the ideal gas. The expansion of the universe like the expansion of the ideal gas.
Very important short remark about temperature. Briefly – the zero point degree celsius (0°C) temperature was chosen by A. Celsius as the temperature at which ice melts or water freezes at a defined atmospheric pressure. 100°C means the temperature of boiling water at a defined atmospheric pressure. These two points are determined by the temperature scale. As well as two points in mathematics, a straight line is determined. O.K. Go on. Scientists (Boyle, Mariott, Gay-Lussac, Pascal, etc.) investigated the behaviour of gases. Change in their volume depending on temperature and pressure. At constant atmospheric pressure, they found a reduction in the volume of studied gases. Air, nitrogen, hydrogen, etc. The reduction in temperature leads to a reduction in the volume of gas. Expressed mathematically — we get a linear dependency — a line with a given direction. How many different gases so many different directions. That was the premise – see the figure below.
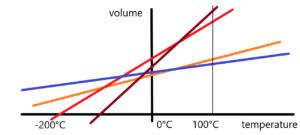
But what was a tremendous surprise was that these divergent directions after their extrapolation meet at a single point, or in a given area, according to the accuracy of the measurement. See next image.
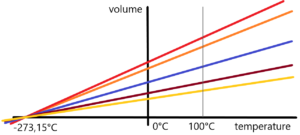
Furthermore, it has been developed on the basis of passed measurements of the theory of ideal gas. This theory works with a gas that behaves ideally – without interfering with internal particles. Light gases such as hydrogen and helium are closest to the ideal gas. But these gases condense at a sufficiently low temperature. Whereas the ideal gas does not condense until temperature, when its volume is reduced to zero. This is equivalent to a temperature of -273.15°C. Temperature absolute zero.
It should be added that this temperature was determined only and only by extrapolating to the ideal gas on the basis of measurements made for real gases.
We also know from the third law of thermodynamics that this temperature is unreachable just like the speed of light in according to the special theory of relativity. But in thermodynamics, we already know negative absolute temperatures – spin systems. This is not a fabrication, nor is it nonsens – it is a reality. On the basis of which quantum generators work – masers and lasers.
Let’s go back to the ideal gas theory. Let’s think of this gas as particles, or zero-size points that vary in their positions. In other words, these points are indistinguishable from each other (as are electrons in physics). We know from Cantor’s theory that one point of zero size can contain infinite points of equal, zero size.
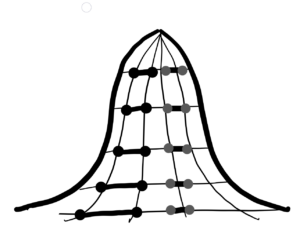
Let’s think of the ideal gas as zero-size points. These points are distributed in a certain volume. When we heat the gas, the volume, that is, the distance among ideal points increases. When we cool the gas, the volume, that is, the distance among ideal points decreases. This ideal gas can be cooled to an absolute zero temperature. In other words, all points will be compressed to one point. As Cantor’s theorem allows us. But we’re in the real world. Individual points (atoms, molecules) are given by three different particles – protons, neutrons, electrons. However, we can reduce these particles to excitations of a quantum field full of vacuum fluctuations. In other words, we can build a model where the ideal points are represented by excitations of the quantum field (“foam”). Call these excitations real points. Real points do not have zero size, however, but they have a certain size in the probability range – see the Gaussian curve of normal distribution with a maximum in the middle.
The entire beauty of the world and the Universe throughout the history is given only and only by the diverse spatial distribution of real points. We get to know this better on the basic atoms of organic elements, where carbon, hydrogen, oxygen and nitrogen atoms make up more than 90% of the basis of all organic compounds – life from protoorganisms, to viruses and bacteria, to complex organisms such as plants and animals including humans. The only difference between a virus and a human is the number and distribution of the basic real “points.”
Optimal temperature in the world between +10°C and +30°C – there are most elements and their chemical compounds in three forms SOLID, LIQUID and GAS – See an image below
There is a rule – the higher (lower) the temperature, the lower the diversity. Not only chemical elements and their compounds but also the diversity of organisms.
But let’s return to thermodynamics. It is not possible to press our real points to zero, or close to zero. Then the energy of one point could be greater than the energy of the entire universe – see Planck’s equation for the quantum of energy E = hf (h- Planck. konst., f -frequency). It is not possible to think of a zero real point size. This brings us to the singularity – zero volume along with infinite energy. Singularity is a very unpleasant state that arises from our ignorance of reality at given level. For we cannot use extrapolation regardless of the basic principles of the existence of real points. Their existence is given by excitations of quantum field in given space. Without space there is no excitations.
A real point (electron, quark) means a vacuum excitation through the entire space of the universe with a given maximum (it makes no sense to wonder whether in the middle). The probabilistic range of particle excitation is the real point. The real point annihilated after a while, and then a new one is created (arises) almost in the same place. The physical process of annihilation and creation. In fact, the real point keeps its position. The rule is, always a new point with a new position nearly at the old point. All the real points are still being restored.
These points form atomic nuclei through the bonding (strong nuclear interaction). The atomic nucleus is a set of varying numbers of real points – from hydrogen to uranium. I do not mention the weak nuclear interaction responsible for the decay of atomic nuclei. The atomic nucleus is a set of real points. From one set with three points – the atomic nucleus of hydrogen, two sets forming the atomic nucleus of deuterium, then four sets forming the atomic nucleus of helium to the atomic nucleus of uranium with 238 sets. Each set has the same number of points – three real points (quarks) with the exchange force of gluons. Thanks to strong nuclei interaction these sets are able to be together. Thanks to electromagnetic interaction, atoms exist – sets of points with “orbiting” points around it. We call such “orbiting” points electrons.
Atoms are the most stable structures in the universe. They’re hard to change. Atoms connect with each other due to valence electrons with given properties. Next, through the elecromagnetic interaction, we have molecules. Let´s call them structures. They are given by sets of grouped real points called atoms. Molecules are no longer as stable as atoms, they split or fuse more easily.
Summary – the real points that are still restored have given properties. Properties of four basic physical forces (interactions). These properties still hold regardless of the annihilation and creation of real points called particles.
The whole world can be reduced to the level of real points with a certain size in the probability range – see the Gaussian curve of normal distribution with a maximum in the middle. These points always have given properties at least in pairs. A real point in itself is meaningless. Given properties – four basic physical forces. Strong and weak nuclear forces, electromagnetic and gravity forces.
The real points interact with each other by four physical forces. But there are limits. Strong and weak nuclear forces keep themselves for a short distance (to the size of real points). But electromagnetic and gravity forces keep themselves for unlimited distances.
Everything – all matter in the universe (chemical elements, molecules, organisms up to the human brain) consists of these real points grouped together into structures of different levels of complexity. The only difference among atoms, molecules, protozoas, organisms or humans is in the amount of real points and structures. Shapes and structures are grouped together into different arrangements (level of complexity) with each other in accordance with given properties (bonding laws). All materials in the world are just suitably grouped interacting structures of real points in accordance with given bonds at each level.
These bonding laws exclude all possible combinations of real points grouped together. Determine the properties of individual structures that consist of simple shapes – real points. These structural properties determine the possible arrangement of atoms in chemical molecules. Not all options can be realized, regardless of given structure properties. They can only be combined into different compounds according to their chemical properties. It is not possible to create all possible combinations. See hydrocarbons – H(hydorgen), C(carbon), O(oxygen), N(nitrogen). How many combinations are possible from the previously mentioned elements HCON (not counting phospohorus, magnesium, calcium, sulphur, etc). Is there a difference between HC or CH? Is it possible to have HC4 instead CH4-methane? See the tree-like structure of hydrocarbons. See methane, ethane, propane, butane. Unexpected tree-like arrangements with increasing complexity.
It is curious how certain very complex structures of grouped real points and structures can perceive and distinguish other structures of grouped real points. Where is the origin of perception and distinguishing? Surely these are not real points in themselves grouped into very complex structures. The origin of perception is to be found in the bindings among real points (given properties). Not only the four basic physical interactions, but also the bonds of higher levels – chemical, biological, psychological, etc.
The mutual arrangement of real points together with their given properties culminates in perception – self-awareness of oneself, one’s limitations and also possibilities. And furthermore, the ability to learn, the ability to obtain experience on the basis of early perceptions, the ability to create the new and previously unsuspected in nature – artworks, musical songs, sculptures, inventions, technical processes, handicrafts, … , etc.
The basis of worldly examples is not an ideal point or an ideal line or an ideal gas, but the basis is a real shape represented by the real point with a probability distribution of its appearance. Every probability distribution is different from another and thus every shape is different to each other. No two shapes are the same, just as no two probability distributions are the same. Likewise the grouping of shapes into different complex structures – from chemical elements, to molecules, to minerals, to organisms, to plants, to animals, to people and their creation – because evolution goes on.
It is impossible to divide probability distributions. Or to examine it using another probability distribution with a higher frequency – hence energy that disturbs the observed subject.
A model of the universe with a suitable distribution of real points can be a muster for a linguistic model. I mean for english language with 26 letters.
There’s one line at the beginning. From this line, we define a segment with a given distance. And we have a basis for shaping 26 letters of the alphabet from A to Z. These letters have the same basis – a segment. The letters of the alphabet differ only and only by changing their shapes. Notice: But if we use e.g letter A 100times or more then every appearance of letter A is slightly different to each other.
We know very well that there can be tremendous amount of possible shapes from one segment then existing 26 shapes (A to Z). The basic requirement is good distinguishability. So we have 26 letters of the alphabet. From these letters we can create a lot of words composed of one or two letters up to 10 or 15 letters. The vocabulary of each language contains a few thousand words for routine frequent use, and a few tens of thousands of words not so often used. Words composed of one or two letters up to 10 or 15 letters could be a tremendous amount. Like with real points there are more and more combinations with appearance of them then basic nearly 120 chemical elements of the periodic table.
Notice: the written word apple, if we use the word apple 1000 times or more, then every word has its own slightly differences to each other like letters. Compare with biological species – see apples. See lots of apple varieties varying in colour, shape and yet they meet the basic definition of a biological apple species. And most importantly, two apples through the history of the world are alike.
Notice: Indeed, all letters of all languages worldwide can be replaced by a suitably shaped section or a few suitably shaped sections (Arabic or Chinese, Indian or Japanese).
In the end every different part of our universe could have the own different word. The word apple represents certain morphological characters that are common to a certain biological species. Likewise, the word snowflake clearly defines the hexagonal arrangement of ice crystals. Although we know every snowflake in the world is an unrepeatable original. Exactly in the same way like two light wavelengths in the line spectrums differs to each other and yet they meet the basic definition of Planck constant.
It is impossible to describe everything. Every shape, every structure and every process differs to each other. How many are different shapes so many are describing shapes. Where to find describing shapes? For better understanding we must make sets with likewise characteristic.
An infinite number of shapes need to be formed, reduced, grouped into a limited number of shapes that will be similar. Create sets of shapes with given properties – common characteristics while respecting the originality of each shape. See maple leaves, clearly at first glance we identify maple leaf. But if we take a closer look at all the maple leaves we have identified, if we look at them in great detail, we find that all the leaves differ from one another. These sets — called biological species change over time. Not only ontogenetically (development of the organism as an individual from germ to adulthood), but also phylogenetically (evolution of organisms through geological epoch) – see clearly visible differences between present-day plant life and perhaps Devon plant life.
Already here we are offered a simple definition of biological species and indeed all natural objects and processes in the world. Easy to distinguish. The maple leaf differs rapidly from the oak leaf or from the lime leaf, or from other leaves. Similarly, a liquid is clearly different from a solid or from a gas. Whereas determining the type of gas or liquid is already harder. But even here, there are methods to clearly divide oil from water or air from steam. And so we can go deeper. This is where the intensity of observational or dividing methods increases. Distinguish types of oils or degree of moisture in water steam. And one can go even deeper. Eventually we come to the conclusion that there are not two exactly the same oils in the world, or two completely identical types of petrol or exactly the same snowflakes.
And on the other hand, we can generalize. Matter comes in four basic forms – solid, liquid, gas, plasma. The only difference between a solid and a liquid or gas is in the stiffness or degree of freedom of chemical bonds. Solid, liquid and gas are common occurrences of atoms. Stable atoms, non-ionized atoms. And that makes this trio (solid, liquid, gas) radically different from plasma. In plasma, atoms are not stable, but atoms are more or less ionized. With free electrons, that is. In the event of very high temperatures, atomic nuclei may fuse or divide.
The basic physical classification of the world
The base of current physics – omnipresent quantum field, that completely fills the universe. This field is the supporting (excitation) environment for the following effects such as radiation or matter. The radiation has no restmass as opposed to matter
Next, we can divide radiation by wavelengths of radio, microwave, infrared, light, ultraviolet, röntgen, gamma radiation. How to further divide ultraviolet or gamma rays? Hard or soft? We can divide the light radiation into pretty rainbow colors ranging from violet to blue to green to yellow to red. And artists can go even further – to distinguish degrees of saturation. But this resolution is no longer done by the machine, by the measuring apparatus, it’s only done by the man because of his perception.
Let’s get back to matter. Matter is divided into ionized and non-ionized. Ionized matter is plasma. Non-ionized matter is divided into solid, liquid, gas. Furthermore, the solids are divided into crystalline, amorphous. Liquids are divided according to viscosity – oil, water. Gases are divided according to their density. And in this way, we can continue to divide up to a point. And that limit is the originality of each observable shape or process.
The basis of all sciences, the basis of all crafts, the basis of all art, the basis of all human activity is a clear resolution. Without resolution and sorting facts, science cannot exist. Distinguishing is also needed in the craft, as well as in the arts.
We are still left with the question where in the chaotic ocean of quantum fields the regular or quasi-regular structures come from. Why they hold together for some time, why they evolve in spite of the surrounding and internal chaos.
Imagine an ocean, an ocean full of different random shapes (a quantum field model with random vacuum fluctuations). In this ocean we suddenly see, we are able to distinguish regular waves, regular shapes and structures and processes among them, which at the micro state are changing in accordance with the ocean, but in the macro state they are stable or quasi-stable (constantly renewed through annihilation and creation). At first we cannot distinguish what it is, but after a while we can recognize the evolution of a shape from its origin, birth through its development to its end. See phylogenetic evolution. In the same way, shapes change ontogenically – by speciation.
For better illustration see – quantum-field-the-basic-state.pdf
See two images below

The first image shows two-dimensional space with the uniformly distributed square points. And the second one shows two-dimensional space space filled with square points grouped in different shapes. What happens if we stretch these two spaces uniformly from the outside? The two spaces will be equally enlarged, including the inner square points. We’ll know the degree of magnification since we’re outside the space. But a possible “flat” inhabitant of the space will not know that his space is being stretched. To him, all the scales inside are the same.
Go on and see the next two images below


At the top left we see no longer a space of squares points, but the space with irregularly distributed variously shaped points. And on the top right we see the space with probabilistic appearance of variously different shapes. These shapes represent excitations of the quantum field. Constantly renewed through their creation – annihilation and creation again, etc. Such excitations are so-called particles or waves. Let us imagine a uniform expansion of two mentioned spaces from the outside. Everything will be the same again, but enlarged. Just stretching the space outside has no effect on the reciprocal changes inside that space.
Now imagine a space defined by chaotic fluctuations. Whether gas fluctuations or quantum fluctuations – it doesn’t matter now. This space expands, or is allowed to expand at a certain speed. For if the speed of expansion were the same as the average speed of the fluctuating particles, the fluctuations would be no more either. The condition for sustainable fluctuation is that the speed of expansion is less than the average speed of the fluctuating particles. Even if chaotic space expands with some speed, there will still be no change in the base units and interrelationships among fluctuating particles, except if the particles or waves are somehow locally bound to their appearance. A kind of local expansion, resp. lesser expansion the other way around.

Sudden blowing up of space in the initial stage – the so-called inflationary process. Certainly, the initial inhomogeneities, chaos, or order are preserved. But these inhomogeneities, chaos or order will no longer be able to interact with each other because of maximum fluctuation speed. See the speed of sound in air, such speed is approximately equal to the average speed of the fluctuating molecules. Similarly, the speed of light in a vacuum is probably equal to the average speed of a fluctuating quantum field – the creation, annihilation and re-creation of wave particles. We can very easily find the average velocity of fluctuating air molecules at a given temperature. We find it because we are outside of the molecules, we are outside even with our base units. But to find out the average speed of quantum fluctuations is impossible. And we’ll never have that possibility to find out this speed. For we ourselves are part of quantum fluctuations, including our base units.
Even if we expand or let expand chaos or order x times, we still get a chaotic or order structure. Thus, we need local changes (expansion, compression, formation, etc.) in addition to global changes (expansion). The local changes must be different from the global changes. Let us now leave apart philosophical considerations on the subject of how stable forms will arise in a chaotic environment – events or changes that are differentiable from each other and “constant” for a certain period of time. The question is how to choose base units in this environment. Base units of time, length and mass. One thing we know, the units must be recognizable and “constant”. Certainly we can take as our basic unit the minimum amount of bound matter or energy – the quantum of energy – the Planck constant h. But even h is not 100% stable. See the “line” radiation spectra of ionized atoms an equation below.
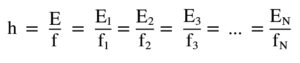
h – Planck. const, E – energy, f – frequency. Planck’s constant h was derived from accurate measurements of the radiation of an absolutely black body, or real black specially shaped cavity. This cavity was heated to a certain temperature at which it emitted certain radiation at a frequency f. The higher the energy E, the higher the frequency f. But this energy as well as the frequency varied in multiples of some minimum amount always equal to h. In other words, the transition between frequencies was not continuous but discrete.
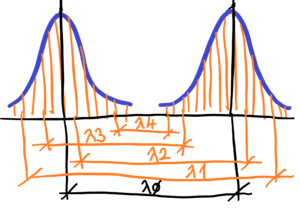
But the most important point is that Planck’s constant is not exactly constant but slightly varies. Its physical magnitude is taken from the peaks of the frequency range of radiation. See the line spectrum of the emitted radiation – they are not exactly discrete lines but sharp Gaussian curves. See a Figure below. There are no frequencies but wavelengts. The meaning is the same.
If we increase the amount of energy at a constant temperature the blackbody radiation will be more intense, but at the same frequency. And vice versa, more intense radiation of a given frequency will not knock an electron out of the metal, but if we increase the frequency of the incoming radiation on the metal, electrons will be knocked out of the atomic orbits – See the photoelectric effect (explained by Albert Einstein).
Indivisible quanta result in recognizable “stable” structures. Without quanta, the existence of chemical elements is impossible. Chemical elements – different atoms combined into the beauty of all nature.
Very interesting topic – to be continued next time
Go back to base units. If we measure in the world, we measure only differences. We choose a clearly identifiable shape as the base unit. The size of the base unit is exactly 1. See a Figure below
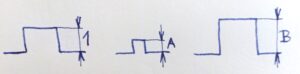
When we measure differences in the world, we measure the difference between the chosen base unit 1 and the measured shape A or B, see from the upper Figure. We do not have external units, constant ones independent of the world and its changes. We only have internal units that change and interact with each other. When we measure differences we influence both the measured and the measuring value. We have no external units available. If we can use the outside as our critical thinking.
See next Figure below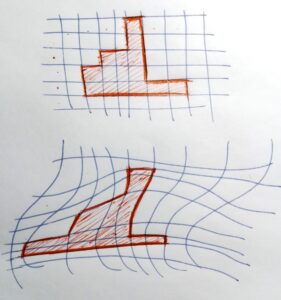
There’s a specific area. In the first case, a regular square coordinate grid. In the second case, a deformed coordinate grid. But we can only see the degree of deformation from the outside. The participant in the deformed two-dimensional space has no way of knowing the rate of deformation. So, local change are important. Local changes in relation to the local scale.
Topology of variable shapes and structures (continuous or discrete, general or local with their interactions).
See a list of pdf files below. There are topics (considerations and suggestions) on the subject of this section here.
| Measurement | ||||
| Base_units_preview | Base unit of base units | Density | ||
| Base_units_2 | Base_units_3 | Base_units_summary | Units_time_space_matter |
