All mechanics is based on solids (or sufficiently bound matter). Mechanics deals only with materials (atoms, molecules) in the solid state. Where there are no solids no rigid bodies, there is no mechanics. You might argue what about hydromechanics or aeromechanics – the flow of air, gases and vapours. Try calculating the flow of a liquid or gas in a completely free space. I repeat in completely free space, without tanks, channels, without earth’s gravity in the atmosphere or magma flow inside the earth, etc. You don’t count anything, or you count everything as you please. Because there are no given boundary conditions – pipe, tank, room volume, water reservoir, gas reservoir, atmospheric envelope of the earth, etc. The boundary conditions are just determined by the solid phase, I’m leaving out Jupiter and the stars, there their boundary conditions are determined by gravity and the different ratios in different parts of those bodies.
In short, hydromechanics (liquids) and aeromechanics (gases) depend on boundary conditions either in the form of classical solid envelope or gravitational forces (rarely electromagnetic forces).
Notice: Also, all organisms are given by solids (along with liquids and gases). There is no organism that consists only of liquids and gases.
Solids are given by chemical elements in solid state like Fe, Sn, Cr, Cu, etc. or their alloys, mixtures or compounds thereof. Their mechanical properties (stress, strain, strenght, elasticity, etc) are given by intolerance of electrons in their atomic shells. All material sciences with their elasticity, plasticity are given by exclusion principle. But it is not enough.
DENSITY – a very peculiar property. Especially to the probabilistic distribution of electrons in the orbitals of
atomic nuclei together with the form of the atomic (molecular) bond. We know that there is a rapid difference between the density of the atomic nucleus and the density of the atom as a whole – that is, the atomic nucleus and the atomic shell together.
Density D means the ratio of mass M to given volume V, which the mass fills. The formula D = m/V , where D (kg/m3), m (kg), V (m3).
It is clear the more mass in a smaller space the greater the density and vice versa. Matter is expressed by its weight and space by its volume. But in the world of atoms, there is one peculiarity – the mass of the atom 99.98 … % is concentrated in a very small area of the atomic nucleus, whereas the rest of the mass (electrons) occupy a much larger space, i.e. volume. Roughly, if we imagine the nucleus as a sphere of about 5 mm, then the atomic “envelope” will extend to a distance of about 500 m or more. Thus, the whole atom is about 100,000 times larger than the atomic nucleus. it is strange that in such a large volume (1 s orbital) there can be at most two electrons. Although theoretically there could be more – see the solution of the Schrödinger equation for this case. But for electrons is valid a special rule called the exclusion principle formulated by W. Pauli. Moreover, the electron appears in a given orbital with a certain probability of appearance. And it is the limits of the probability of appearance of the electron or electrons that give the final volume occupied by the atom as a whole. When we think of it, it’s like a very very dense poppy seed placed in a large balloon. See below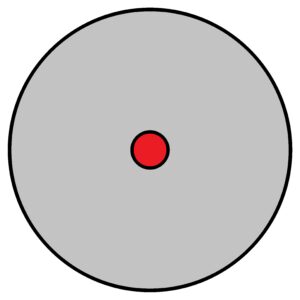
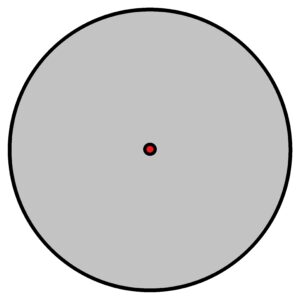
And imagine interstellar space, where hydrogen or helium atoms are a few tenths of a millimetre in size. That’s how powerfully its electrons are excited, in such vast volumes. See above, image on the right.
Anyway, instead space e.g. certain volume like a sphere imagine a line, resp. section on the line. The section on the line will mean unit mass (weight) and unit space (volumes).
Volume resp. the section with unit mass in given space (distance) has the density 1. When a section expands (until N distance), its density decreases. It’s the same with atoms, we add units of mass in the middle and increase the distance of the orbitals. But not in a linear manner. See below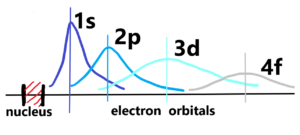
In the centre there is a nucleus (red). The size of the nucleus is very very small compared to the size of the atom, or the range of electron orbitals. There is an extremely difference in the density between the nucleus and the orbital. Atomic nucleus has nearly all atomic mass concentrated into very small volume in spite of electron orbitals, where the near-zero mass is distributed over almost the whole atom. If we can neglect the mass of electrons relative to the mass of the whole atom, then we can neglect the volume of the nucleus relative to the volume of the whole atom. That means we can consider the mass of the nucleus to the volume of the whole atom. Therefore, to determine the density of hydrogen atom with an orbital 1s is very delicate. Because the volume of the hydrogen atom has a probabilistic range, just like all other elements with next orbitals. Especially see the elements with orbital 4f. Every atom of the same type differs to each other. The cause is – probabilistic resp. indescribable appearances of electrons in quantized orbitals. Quantization results in clear, definable differences between energy levels. But these differences cannot be expressed in absolute units, but are relative to each other at the atomic level.
Notice: The boundary of an atom does not end at a precisely defined distance, but rather decreases indescribably toward to zero (0) according to a probabilistic course. In other words, the boundary of an atom extends to infinity, or to the level of fluctuations in the matter (quantum) field. There are no sharp boundaries.
BTW: How to measure the density? E.g. density of H2 or O2 or N2 or H2O. In relation to what? To the vacuum? Let’s release e.g. hydrogen or nitrogen into a vacuum and …. and nothing, the gas will expand with a speed depending on its initial temperature. Plus, the hydrogen atom will get bigger (see previous mentioned excitations). So in a “vacuum” we measure nothing. So we must have the gas enclosed in some kind of bottle. And where do you get a bottle? From solid hydrogen? Hardly. Then we need the bottle made of another element, like Fe or Cu or Sn. Only now can we can measure pressure, temperature and density. Actually, we can’t, we have nothing to do. So we have to have two bottles of Fe, with N2 inside. One closed gas bottle will be the reference (unit) and the second, or other closed gas bottles will be the measured ones. Instead of a closed embrace, we can also have a gravitational body like the Earth and the gas will be held to the ground by gravity. Only the pressure of the gas will decrease with height.
Very peculiar property the density – especially of atoms or molecules. It is impossible to measure density of something relative to vacuum. Only to measure the density one atom to each other atoms. So, the density has also relative value.
H2O in vacuum … ? There have to be some closed box, or another gas or a strong gravitational field. Only then can we observe the transitions between gas (steam), liquid (water) and solid (ice). Which means that density is highly relative. Not just atoms, but also molecules.
However, back to the density measurement. We know that the density of an atom is a rather uncertain value – we know the mass of an atom, but its volume is inaccurate. It should also be noted that the density of a substance consisting of the atoms of a certain element strongly depends on the arrangement of the atoms in the crystal lattice in solid states, and in the different types of bonds in liquid and gaseous states. There is also the influence of temperature and pressure. Briefly we can imagine atom like a foam polystyrene (after expanding). There is only 2 – 3% of solid matter and the rest is the air. See below
The same (principial) distribution is everywhere around us. See astronomers with graph showing the distribution of matter in the universe. Roughly 3-4% is matter in the form of stars, planets, nebulae, galaxies, and mainly intergalactic matter, with the rest falling into the category of dark matter and dark energy. Similarly, the distribution of water on Earth: less than a tenth of a percent is the amount of water in rivers, lakes, etc., with the rest falling into groundwater, air humidity, and, above all, the seas and oceans. And so we could go on. Everywhere in nature, we can observe the structure of an inflated balloon with a core inside or the structure of polystyrene foam – see the irregular structure of metagalaxies in space.
See the entropy – incerasing volume and decreasing the energy (mass).
… to be continued
To read more about springs – ELASTICITY in the case of springs
Imagine to connect huge number of springs with extremely high k e.g. atoms with their electron´s orbitals, then we obtain quite real value of Kc – see different solids like metals together with Hooke law. This is only for rougly illustration. In Reality of materials it is more complicated.
Thermodynamics – mechanics of chaotic behaviour of particles
The basis of thermodynamics and indeed of the whole world is chaos. Chaos in a closed space. Chaos of moving particles, molecules, atoms. This chaos can be converted into mechanical work by the controlled expansion of initially chaotically moving particles. See an engine piston or a turbine blade.
Let’s have a model – a closed box with N particles. Initial conditions – all particles have the same velocity. After some time we find that the velocities of the particles are different from each other. The speed of movement of particles in a closed space varies – from almost zero speed to maximum speed. There is a kind of average particle velocity that is close to the value at the initial conditions.
the velocity distribution of particles depends on :
– the volume of the box
– the size of particles (very interesting model with particles like ideal points with zero size – these never meet each other)
– the number of particles
particle size is relative to the size of the box
The rule is – the higher the speed – the shorter the duration. The same for the lowest speed. If we want to keep the lowest velocity or high velocity of a particle for a longer time – we would have to isolate the particle from other particles. Perhaps by expanding space or otherwise. See the rubber sheet thermodynamics in two dimensional space below.
See the image below – thermodynamics of rubber sheet, resp. of elastic membrane
Thermodynamics of rubber sheet – elastic membrane full of chaotically moving particles. The disadvantage of isolating a particle is that we can keep its velocity for a longer time, but we cannot change it. Thus, it would be better to adequately stretch the elastic membrane according to how we want to accelerate the particle or, on the contrary, to decelerate it. Which leads to very interesting results.
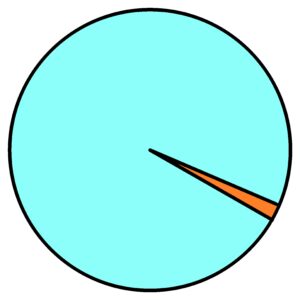
Go back to thermodynamics before we begin to solve the thermodynamics of an elastic membrane or an elastic volume. How to describe purely chaotic processes? It is impossible to use mathematics. Mathematics doesn’t have a chance in the case of pure randomness. Mathematics has nothing to go on. But thermodynamics exists in clearly given mathematical equations. So the equation pV = nRT, very familiar equation for engineers. Sure, but there are differences. If we have one chaotic environment, we won’t be able to study anything, we won’t be able to describe anything, and we won’t be able to predict or verify anything. See first image below – only one chaotic environment.


So we need to have at least two different chaotic environments. One environment will be the chaotic motion of air molecules in the atmosphere and the other environment will be the chaotic motion of molecules in a closed cylinder with a piston. See a second upper image.
We will ignore temperature for the first time and examine what is called pressure and volume. It is possible to think like this and mainly to measure – volume and pressure – the weight of the mass relative to the given piston area. We obtain the equation p1V1 = p2V2. The multiplication of pressure and volume before expansion is equal to the multiplication of pressure and volume after expansion. Let us remember that we only know ratios and not absolute values. What is the absolute value of chaotic motion – relative to what? Relative to zero? Relative to what zero? To the zero of particles? But zero is not even in a vacuum – see the exclusion principle. Not to mention – relative to zero, everything is infinity! And each unit we have chosen as the base unit of measurement is just a chosen ratio, the ratio between the measured value and the chosen (unit) value. Very important remark for next consideration in thermodynamics – expecially absolute temeperature, absolute pressure, absolute volume, absolute energy, absolute entropy, absolute enthalpy, etc. But the most important remark is about at least two chaotic environments with different characteristics to each other. For example, the expansion of the piston inside the steam cylinder, which is surrounded by dense, viscous oil , such expansion is different to the expansion of a piston inside a steam cylinder in an ambient atmosphere. Not to mention the change in the viscosity especially in the case of a non-Newtonian fluid.
See a cylinder with moving piston inside it. There are two different chaotical environments. See image below.
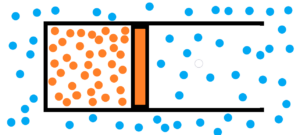
1) atmosphere filled with chaotically moving gas molecules – see blue dots
2) chaotically moving gas particles enclosed by a piston in the cylinder volume – see orange dots
Both the gas and the surrounding atmosphere are purely chaotic environments. In both environments, molecules collide. But in the case of a gas, we see that the collisions among gas molecules are more violent and more frequent compared to the molecules of the surrounding atmosphere. A gas enclosed by a piston in a cylinder will have tendency to expand relative to the atmosphere until the violence and frequency of collisions among the molecules are equal. Not to mention the final damping oscillations. See image below.
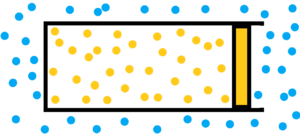
How to measure how to evaluate the violence and frequency of molecular collisions?
Some base units need to be chosen. See next image below.
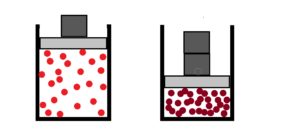
To put a unit weight on the piston. How many units times the frequency and violence of collisions. At least for the beginning.
Rocket propulsion
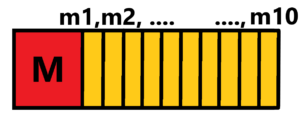
We will not discuss the theory of reactive propulsion arising from the law of conservation of momentum on the basis of third Newton´s law. At the beginning there is the mass of the rocket which is equal to M+m1+m2+ … +m10. Where M is nett weight of an accelerated satellite. While the sum of m1, m2, … , m10 is the weight of the fuel (propellant). When we want to accelerate a body M we have to rebound from something – the ground, water or air (propeller). We have nothing to rebound from in a vacuum. We need to take some propellant with us. And that’s a big problem – because of the maximum speed of the rocket. I mean, the more fuel we carry with us, the more fuel we have to burn. The only possibility is to increase the outlet velocity of the combusted fuel. The higher the velocity the higher the reaction for a given weight of fuel.
There is a valid equation: Mv = mu, where M is the weight of rocket with its velocity v and m is the weight of fuel with its velocity u.
Of´course M means M+m1+m2+ … +m9, then M+m1+m2+ … +m8, … , until M.
So we use the maximal speed in the universe, the speed of light. Then there is a possibility to use interplanetary or interstellar matter at a density of, say, 3 hydrogen atoms per cubic centimetre. Especially if we use an extra large funnel that will collect those hydrogen atoms – alias stabilized grouped quantum field excitations into the form of a hydrogen atom. See below 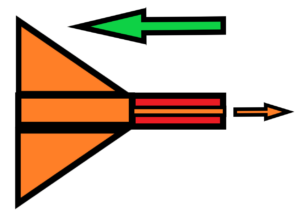
where the green arrow means the dirextion of the interstellar flight and the orange arrow means the speed c of photons from the accelerated rocket.
There is another criterion – maximum acceleration because of the strength of the material or the strenght of pilots inside that rocket.
Kinematics is about degrees of freedom in the movement. No degrees – no free movement – see statics. When force is also acting in the movement, we reach dynamics.
straight movement
rotational movement
oscillating movement
to be continued next time …
Steam engines, turbines, pumps, motors, details as valves, propellers etc.
| Download | Download | Download | Download | Download | Download |
| Part_engines_I | Technical drawings | Water turbines | |||
| Heusinger timing gear | |||||
