It is difficult to accurately describe real circumstances in nature or technology. We can certainly determine general equations, see thermodynamics, with an accuracy of tens of percent. The rest can be fine-tuned ‘by trial and error’ based on estimates, experience, and measurements—see the design of heating networks, etc. And if we want to determine the thermodynamic state to an accuracy of a few percent or even less, then we need to know the surrounding circumstances perfectly and use advanced mathematics. But the rest always has to be fine-tuned experimentally. This applies for thermodynamics, mechanics in general, for assembly of a synchrocyclotron, and finally for the start-up of a production line for sheet metal, integrated circuits or anything else. At least fine regulation is always necessary. Such is nature, indescribable in detail, incomprehensible – even though there are given frameworks such as basic physical formulas that can always be verified, especially under so-called ideal conditions. However, these conditions are artificial, achieved at the cost of efforts to isolate them from external or internal influences. Therefore, predicting what will happen in nature (or now in technology) in the distant future on the basis of more or less complex mathematical equations is as absurd as deriving what happened in the distant past.
See also the stability of the planetary system, which appears to be the ideal “material” for celestial mechanics, but which is subject to (internal and external influences) indescribable changes over tens of millions of years. The position of the planets will then deviate by tens to hundreds of percent from their current state. Compare the predictions of billiard balls after x mutual collisions – for the first tens, if not hundreds, of collisions, we are able to determine the position of individual balls with sufficient accuracy. But as we know from very accurate measurements, the difference between the predicted movement of the balls and their measured value increases slowly but steadily. Until we reach a state where the angular dispersion is more than 90°. Not to mention the legendary three-body problem in mechanics (H. Poincaré).
In short, mathematics is the best, safest, most reliable, most powerful and also a very beautiful tool to describe nature and technical processes. There is no better servant and there will never be a better one. But this best servant becomes a very dangerous, deceitful, misleading, brutal and unscrupulous master when used carelessly!
Mathematics or geometry is taken from nature and not the other way around! Geometry (mathematics) abstracts from the myriad complicating circumstances, thus becoming an impressive, internally consistent, and complete theory. It cannot claim unlimited applicability in the study of the material world. This abstraction also allows the general and profound properties of material things, which we call spatial and which we interpret in geometry, to appear in their pure form. The laws of geometry are therefore laws dependent on nature, since they are taken from it. If the accuracy of such research exceeds certain limits, then geometry—by its very nature only an approximate reflection of reality—is no longer adequate. In order to be usable again, it must be made more precise in accordance with new experimental facts, returning to what was set aside along the way, from which abstraction was made.
What is mathematics? Counting. Counting what? Counting numbers. What does mean the number? What is the number? The definition of number cannot explain the nature of itself as a change of form or event. The number represents something distinguishable – a distinguishable form or event, which has been greatly simplified by the abstraction. To use numbers means to distinguish forms or events from each other and then to abstract one form into a number one (1). Number 1 means the quantity or size of something distinguishable and abstractly reduced. Maths increases from „stabilized“ forms and events, from renewed stabilizations of distinguishable forms and events. And math needs these stabilised forms and events. Distinguishability over time – distinguishable objects, processes or feelings must have a certain duration – they must be stabilized. See e.g. biological species (difference between Devonian nature and present nature), if biological species were changing rapidly we would not count, name, evaluate them. Mathematics has no chance against randomness. See thermal motion of molecules or quantum fluctuations – see images below, there are no stabilized shapes


Nothing to hold on, no reference point. There is no form to abstract. How to determine the reference point, how to determine the structures inside such fluctuations? Roughly written – what in the above images will we calculate, what will we distinguish? See also below the course of a randomly deformed line with many local peaks.![]()
Hard to differentiate in the above environment. Everything is changing, bubbling. If we measure one side of a given area, the other sides of the area have changed. So there is the first condition – stabilized forms, shapes or structures. See below![]()
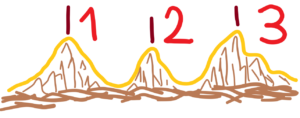
There are three clearly recognizable shapes-peaks. The other three shapes are at the limit of distinguishability. They either evolve into orderly shapes or disappear as part of a chaotic background. It is quite hard to keep stabilized shapes-peaks in chaotic environment. Why count something that can’t be counted? What doesn’t come from clearly distinguishable shapes or appearances with their peaks (orange marked). See below
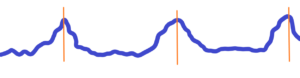
But, really, how many peaks are there? Is it really three? Actually, there are many more local peaks! See, for example, the fractal course in the real world. Mathematics is the product of Reality, of more or less temporal (renewed) stabilized chaotic appearances in the chaotic environment. Such appearances have temporary peaks which are slightly changing. These peaks are condensed (replaced) by mathematical abstraction into ideal points with zero size. (So-called the singularity). But there are no singularities in nature at all. There is always a range, a tolerance or at least the slightest fluctuation around a “value”. No matter whether it’s an engineering dimension, wavelength, or vacuum fluctuation.
Recognizable shapes, stabilized forms over a certain, sufficiently long period of time, are the origin of Mathematics. They are and they are not. It takes someone to distinguish these appearances, give them names, and then can they be counted. After that comes pure abstraction, where one appearances resp. its peak becomes the number 1. But all appearances (forms) differ in their shape from one another. So it is necessary to make these forms into clearly distinguishable shapes – see the difference between apples and pears. Admittedly, each apple is different from the other, but they are clearly distinguishable from pears in their basis – common characteristics.
Maths is about two extremities of nothingness – zero size of an ideal point and infinity stretchness of an ideal line. So two extremities have common denominator – emptiness without any shapes. There is no chance something to distinguish. See below

These terms (ideal point or line, etc) were created solely and exclusively artificially—through abstract thinking. See reduction of dimensions to zero into so-called ideal point. The same applies to an ideal line. BTW? The ideal point doesn´t exist, only its name or its mark. The size of the ideal point is exactly 0, resp. 0,000 000 000 0.. … … 0 until infinity. Where was the point size derived from? From the size of the unit section (distance or interval). See the top picture. The unit distance is defined by two points 0.000 000 … and 1,000,000 … with a size of zero. The size of the point is derived from the unit section, and at the same time, the points define the unit section! There is an contradiction like in many parts of mathematics. How to mark out a section on an ideal straight line? All shapes in Reality have indescribable (probabilistic) appearances. There are no ideal points or lines anymore. See below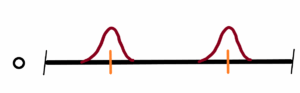
Very interesting are the ratios, or the limits defining the given interval (section). A large or small interval does not make sense on its own—the size of a limited interval must always be related to another limited interval. Finiteness (limitation) to a different finiteness (limitation). It is always a relative value. On an ideal infinitely straight line, we limit a certain interval—a unit section. See below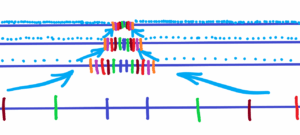
The base interval is marked with blue lines. Such interval can be taken as a value 1. We can place other intervals on the infinite line, see the green interval or the even larger “brown” interval. And so we keep going to the infinitely large one, or keep getting smaller and smaller and continue to the infinitely small one. But the basis is already given – the blue interval with size 1. Now the question, what is the actual size of the blue interval? Relative to what? Relative to infinity, or relative to the other intervals. The size of the blue interval is still 1. Regardless of any changes. After all, another interval (green, brown or red, or others) can take the size 1. And all these intervals can divide infinitely times to infinitely small and grow infinitely times to infinitely large. Does this mean that relative to each other the different intervals are equal? They are not, blue will always be smaller than green. But relative to infinity, it’s not. Given the infinity of the expansiveness of the so-called ideal line, or the “infinity” of the so-called ideal point of zero size. Intervals make meaning relative to themselves (distinguishability), but relative to infinity (or zero) it’s different. We can work with the interval as we like, but the interval carrier (infinity) is independent.
There is a given interval. By dividing this interval into smaller and smaller intervals, we can define smaller and smaller intervals ad infinitum. And vice versa, we can multiply the section until we reach an infinitely large section. Finality is connected with distinguishability, infinity changes (infinitesimals) are connected with Continuity. Distinguishability is always changing in the world. Faster or slower changes, but there are always changes. Numerable changes at macrostates like particles, atoms, molecules, minerals, organisms, etc.
Without limits (boundary conditions) there is no chaos, no temperature, no frequency, no energy, no mass, no quanta, no changes, no space at all.
So biggest changes are powerless to their limits respective to the Originator of limits.
Mathematics means a reference system based on unit squares – distance between sides of unit square is 1. These unit squares are connected together at corner points. These points are ideal points with zero size. Similarly, the sides of squares have unit (1) distance and zero thickness – in short they are one-dimensional. See below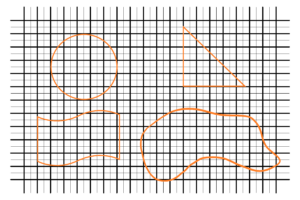
The reference system upper illustrated above is used to describe different forms, shapes and events – in orange. We can easily describe different squares, rectangles, and all shapes based on squares. But shapes that don’t have a linear progression, such as the circle, ellipse, and various curves, so there will be a big problem of how to express them, to describe them by using unit squares. There will already be a small problem with the triangle. Certainly the area of a triangle is half of the unit square, but the problem will be with the hypotenuse of the triangle, which is not so easy to describe, to express, the square root of two. Mathematics is unable to express this kind of number. The unit square is also the origin of indescribability, inexpressibility by itself. No mention other non-squares forms and shapes (orange marked). To desribe precisely a square by a circle or vice versa to describe precisely the circle by the squares – it is impossible. In the same way how to describe the originality of of one individual, form or event, to describe the originality of one by the originality of the other. This is impossible despite the fineness of the resolution. E.g. to choose a nema from set of differents names and by this choosen name to describe (evaluate) other names?!
The finer resolution of the grid (squares), the division of the units into tenths, hundredths, thousandths, results in a much better resolution and thus a description of the orange marked shapes. But that’s a mathematical idea, but it works differently in nature. But … as the resolving power of the microscope grows, i.e. using much shorter wavelengths, the possibility of influencing the observed forms, shapes or events also grows by much more energetic wavelenghts (particles).
BTW: Where did come the grid of ideal squares from? Such grid is not observable in the world, any more!
Let´s see the logic – there are three shapes (see upper image) A=1, B=2 and C=3 – we assume by logic if A<B and B<C then A<C. That looks right. But we forget about the course of shapes and the measurement process, and also the condition of the simultaneity. Firstly, the shapes can change during the measurement, secondly, we can measure out of the peak of the shape, and secondly, it depends on the observer where two events or shapes looking simultaneous may not be simultaneous. It is better to write in probabilistic form if P(A)<P(B) and simultaneously P(B)<P(C) then P(A)<P(C)
No matter what the shapes are, they must be stabilized for a certain time period. Only then does language begin – sorting shapes by their common features and naming self-similar shapes. Then the mathematics begins, see set theory – identify the set of given shapes and classify corresponding names. Then can we count the number of given shapes. See below
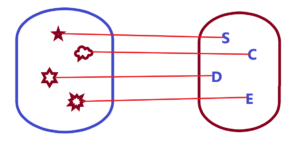
Mathematics like gravitational law is tightly connected with separated and stabilised forms and events. Gravitational law like other natural laws. Such laws are based on separated and stabilised forms and events (processes). How to discover and formulate natural laws? For example, the law of gravity. Only by observing of stabilized processes. Based on observation of planetary orbits and further abstraction. The planets are replaced by ideal points of certain mass. Or the size of the planet is unimportant in relation to the distance from the sun. We can solve the orbital periods with sufficient accuracy. But the situation is quite different in the case of dense nebulae, forming planets – planetisimals. Differently shaped masses. See below
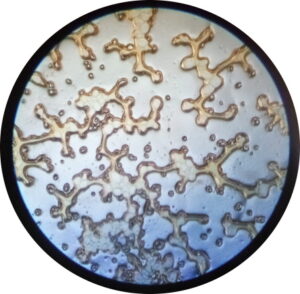
How to formulate the law of gravity in the above two environments? Chaos and more chaos. Sometimes pretty, sometimes ugly, but still just indescribability, nothing to catch onto, no reference point, no two same ratios or relationships for a certain amount of time. Laws are results of separation. See how is impossible to derive gravitational law from chaotic circumstances. O.K. We have orbits of planets like the result of separation and stabilization. We derived the gravitational law. And with the help of this law we will solve, i.e. predict the behavior of more or less stabilized bodies. Finally, perhaps we dare to calculate the behaviour in the above two chaotic environments. We will use the infinitesimal calculus, we will use the quantity dM, then the variable distances D. We will set the boundary conditions and make the calculation for the future evolution with some accuracy, which we will verify on real models. But the derivation of the law of gravity was done on clearly separated and stabilized forms and events – see the orbits of the planets. And suddenly we will use this law for unseparated and unstabilized forms and events.
It is also important to know that even the motions of the planets, although they appear to be very stable, are not that stable – meaning tens or even hundreds of millions of orbits around the Sun – years in the case of the Earth. Not only the complex orbit of Mercury, but also the movements of the continents on Earth, which affect the inclination of the Earth’s axis, and especially the interaction of all the planets and their moons. So the prediction of what the situation of the planets looked like e.g. 100 mil. , is very blurry, as is exactly how many 100 million years ago – especially each year (the period of the earth’s orbit around the sun) has a different period.
If we were able to measure the orbits of the planets over a long period of thousands of years, we would find deviations. Deviations from current predictions based on the equations of celestial mechanics. Just as we find deviations in the periodic rotation of the earth on its axis. If we accurately measured the motions of the planets over much longer than just thousands of years, say hundreds of thousands of years, or millions, the measured deviations would be high relative to the predictions. In other words, an update is needed, a correction after a more or less extended period of time. Finally – without regulation (or self-regulation) there is no stabilised natural or technical process. The influence of an omnipresent chaotic environment that still affects.
In the lower “illustration” of the matter (quantum) field there is nothing to distinguish or to describe – everything is always changing indescribably. There is no point in describing let alone evaluating the differences – every course is purely random. See below
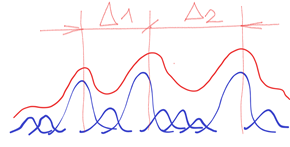
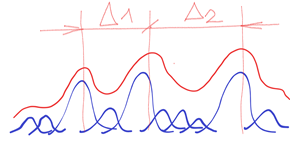
But it is quite a different case when in a chaotic environment there are also chaotic “came out” forms, but clearly distinguishable, also indescribably variable (black marked), but clearly interpolated by the continuous course of the normal frequency distribution (orange marked). See below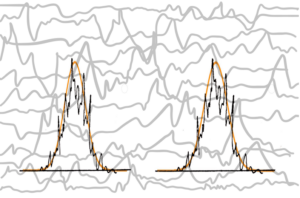
These “came out” forms, though also chaotically variable, are constantly renewed in more or less the same range of the interpolated orange course. Now we can start with the resolution, description and evaluation. Thus the two interpolated courses of the two clearly distinguishable forms make the basis of the following description. See below
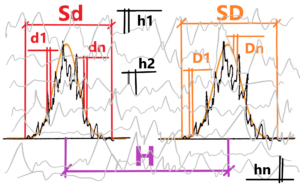
Both interpolating courses are limited on the left and right. Sd and SD. The limitation means the boundary with the surrounded chaotic fluctuations. But these fluctuations also form the interior of the “came out” forms Sd and SD. Each inner part is different from all the others. See d1 ≠ d2 ≠ d3 ≠ … ≠ dn and D1 ≠ D2 ≠ D3 ≠ … ≠ Dn.This is as true as in “came out” forms as in surrounded chaotic environment. h means characteristic space (“size”) for smaller part of chaotic fluctuated environment. There are infinity such spaces h1, h2, …. , hn where n = ∞ then h1 ≠ h1 ≠ h3 ≠ … ≠ hn
But certain relationships must be valid for the sake of clear resolving (differentiability) – firstly the value H – space between two peaks of Sd and SD. Then H > Sd + SD or 1/2 (Sd + SD) – or the exact formula for resolving power between two peaks in optics.
Temporary conclusion:
Certain “came out” forms are allowed and supported in their restoration, others are not. See e.g. differences among apple vs. pears or among allowed orbits of electrons in atomic shells.
See next illustration – every electron jump after excitation from a higher level (shell) to a lower level (shell) in unique way, (the influence of omnipresent pure chaotic environment like quantum field) See below line spectrum with probability distribution of emitted radiation with two peaks.
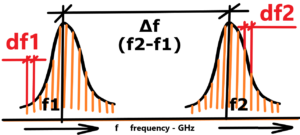
No two wavelenghts are alike. No two wavelenghts has same size. But they have a common denominator – Planck’s constant. Roughly written – Planck’s constant is the peak around which the wavelengths of emitted line spectrum radiation are piled. Planck’s constant slightly changes depending on the “pile-up” of emitted photons
Every wavelenght is unrepeteable original. We can certainly approximate the wavelengths of the emitted radiation in number to a certain number of decimal places. And for calculations with any accuracy, this is necessary. But let’s keep in mind that each wavelength is a non-repeatable, irrational number.
The same is valid for the appearances of apples and pears in the world. No two apples are exactly alike. It is the same with apples and with all biological species, and indeed with all shapes in the universe – each atom is slightly different from one another, just as one vacuum fluctuation is inexpressibly different from another. See below – “quantized” differences between apples and pears
Apples and pears are easily recognizable from each other. This is also valid for the most untypical apples or pears.
Mathematics needs differentiable shapes, structures and processes. Even more, mathematics needs stabilized differentiability. Clearly defined differences over time. Without stabilized differentiability (distinguishability) there is no mathematics, no language, no science. We perceive the world around us and inside us by our five senses. We distinguish different shapes and objects in Nature, the intensity of feelings and much more. We express these distinguishable shapes, structures and feelings in some way. And we do this in three forms – gestures, voices and images. Gestures have remained and language has been developed from the voices. And from images, writing has evolved over time. We get names – by voice or in writing. Names of self-similar objects, shapes, structures and feelings. Self-similarity – the basis of abstraction. To abstract from details to common characteristics. See the difference between an apple and a pear (though every apple and pear is a non-repeatable original). After that came mathematics. The next level of abstract thinking. To determine the quantity of objects, shapes, structures or “feelings”.
The problem with mathematics, like language, is that it calculates, distinguishes only and only existing objects, shapes, structures, processes or feelings. Roughly speaking, it is behind development. Behind the creative abilities. Mathematics, like language, does not calculate, does not name ideas, that which arises, that which is born in the mind, or that which is realized. Whether new objects, shapes, structures, processes – we call all this craft, artistic or scientific activity. Mathematics, like language, cannot tell us what of the “pile” of ideas and intentions will be useful in the future. For this, there must be experience. Experience that cannot be calculated primarily. An experience whose results can then be counted, analyzed, evaluated, predicted over a period of time before an unexpected event, idea, trend, process, object, etc could appear. In short, there is a new event, a previously unsuspected or only slightly suspected event, previously marginalised by abstraction. This event then greatly disrupts or cancels all the most complex calculations, evaluations, analyses and predictions.
We are at the meaning of mathematics – to lead us through our experience to ever greater or gently perception, to distinguish the previously indistinguishable relationships and not to settle for the currently distinguishable, perceptible and calculable forms aor events. E.g.: How to find out what will be created? That which will be created in differentiated forms and therefore nameable and therefore countable. After that we can do mathematics with all its more complex processes.
There is an “ocean” of matter field full of random fluctuations. Inside this field there are constantly renewed appearences of what we call matter in the universe such as elementary particles, chemical elements, molecules up to all matter in general including living organisms. These appearances have different and still different shapes within a given framework. Nowhere can we find the so-called ideal point, the ideal course of the frequency of appearences. All these ideal courses are just the result of human abstract thinking. Here we find the origin of number and thus the origin of mathematics. See below
There are three clearly distinguishable courses. Every course is replaced by the number 1, 2 and 3. There is also a given distance between points 1 and 2, or between points 2 and 3, or between points 1 and 3. As we know these distances is changing. And after a very long time the distances can change completely or disappear together with the boundary points.
So-called pure mathematics calculates with ideal points which have zero size and which have a given distance between them. These ideal points were created by purely abstract thinking on the basis of the above-mentioned courses. Mathematics is a product of grouped random events, not their source.
It should be mentioned that in nature, all natural forms and processes are always and always determined by more or less different courses of frequencies of their appearances. In nature there is not and cannot be an ideal point or an ideal distance. These are only helpful and necessary constructs which must be constantly updated according to the actual state. Mathematics cannot explain the origin of Reality, the origin of Nature in its great diversity. But Mathematics is the best tool to solve current problems in science, engineering and all humans endeavour if mathematics is controlled by man with his perception and experience.
In Nature there are no singularities – so-called limits states close to zero (0) without any limits. In Nature there are only different and variable courses of appearances so-called probabilistic or frequency distribution like Gaussian course. As we metioned previously, these appearances are the basis of mathematics. Then by abstract thinking we choose the peak of certain appearance course as a point with number one (1). Then other peak of next appearance course as a next point with number two (2), etc. These peaks, now called points, have the size exactly equal to zero (0). So these are the ideal points with zero size in pure mathematics. There is a given distance between these ideal points. Such distance have to be also the ideal. But between what distance? How to reach zero? To reach points with 0 size? How to reach nothing? That nothing can be anywhere. How to define the exact position in spacetime for nothing with something distance. Where is the reference point? Such ref. point have to behold on some existing and definable forms or events. How to define non-perceptible boundaries? See also irrational numbers – there is no possibility to define them exactly. OK. You can say for ideal math these questions are irrelevant. But the opposite is true. Ideal distance between two ideal points is a contradiction. Something against nothing.
Then it leads to discussions about how many points can fit in one point (of course infinity if they have zero size), how to define the difference between distance and point when distance is something and point is nothing and much more. But distance (something) is immensely different from a point (nothingness). Certainly Cantor’s and Hilber’s mathematics of sets makes sense applicable to reality, but as a helper not a tempter. See different cardinality (magnitude) of infinities, etc.
Mathematics is a special kind of ignorance towards its foundations from which abstractions came – namely the replacement of more or less variable forms grouped into a certain course with a certain peak (maximum), which, moreover, is always changing, in short, the replacement of it all with one point. Mathematics equals (summarize) events and entities which are not exactly equal to each other. To give the name to set. After that there are the number of elements of every set. To count 20 flowers is OK. But to explain the origin of flowers by dividing their parts without observations is impossible. We only get the indescribable rest like chaotic quantum field. The end of our knowledge. But that´s not truth! It is the beginning of next knowledge – the experience with invisible but feelingable movements (desire, intentions).
Let’s do away with math when everything is unique and unrepeatable? Then mathematics is meaningless? But whatever! Mathematics will continue to be used. I repeat use it in accordance with observation and verifiable models. For there is no better servant, evaluating and directing servant than mathematics. Yes everything is unique, even in the smallest way that can rapidly change. But it is for evaluation and reflection that mathematics serves us. Reality is more than mathematics and that must be respected.
Certainly existence of irrational numbers – such numbers are the expression of the origin of all numbers. They are abstract from Reality – ideal point, ideal line, etc. Ideal whole number one, two, etc. with noughts until infinity before and after the decimal point. See ….00000000000000000001,0000000000000000000…….
The Logic of of Reality is different from the so-called ideal logic. Just as Reality is different from ideal so-called pure mathematics. If a is greater than b and b is greater than c then a is greater than c. This is true in ideal logic, but in Reality the ratios differ not only in content but also in form – current events.
Stabilized formations – the beginning of natural processes and beauties. Stabilized formations – the beginning of mathematics, logic and all kinds of sciences, crafts, arts and technics.
Abstraction is a double-edged weapon. On the one hand, abstraction is a great simplification and reduction of the situation – the current state of the existing situation. But on the other hand, abstraction is a great carelessness towards the origin, towards all relationships, towards evolution itself, towards all changes.
For to identify, to abstract what is main and what is secondary in a given situation, and at the same time to verify it, is the greatest ability of human thinking. But it is also a great temptation to rely on the degree of abstraction achieved. And this because of laziness, inability or loss of flexibility of thought and perception.
Nothing against abstraction, quite the opposite. Without abstract grouping of events according to common marks, without this abstraction, one can go no further, to have a knowledge. But it is also possible to lose one’s way in a world of unreality and vain fictions if we forget the source of abstracted events. These can lead to idealization, to idolization of limited abstract thinking with all problems for humans society including Nature at all. People are blind at two extremes. The first extreme is the blindness of chaos, the impossibility of abstraction. To be carried along by chaotic behavior. The second extreme is overuse of abstract thinking, without respect to the origin of abstraction, without respect to the whole, to the whole interrelationship among abstract processes that interact with each other along with their origin. It does mean reciprocity among free and grouped events.
Just abstraction directs us to Reciprocity always different and more.
Imagine the closed box with two horizontally spaced walls. The ball will bounce repeatedly between them See below
The measured position of the ball is in the middle. The direction to the right shows the future and the direction to the left shows the past. It is clear from the image that the position of the ball, or the uncertainty of its position, increases both to the right (future) and to the left (past). The degree of uncertainty depends on many conditions – the shape and quality of the ball and walls, their mechanical properties, etc.
There are three possibillities
1) in the past – everything is hidden in chaotic behaviour
2) in the future – everything is hidden in chaotic behaviour also
3) the actual state, with some uncertainty in the future or into the past
But this process (the ball between the walls) is not alone in the world. When there is no outside influence on a given process, we are able to predict the immediate future of the process very accurately and to make a rough prediction of the more distant future, but long-term predictions or estimates of the distant past are completely out. Not only because of the limited accuracy of the model, but mainly because of the influences of surrounding unexpected events. See thermodynamic – How to predict the path of a particle in a chaotic gas? What will be the quality of the prediction? Because the density of the gas, the density distribution of the particles, matters a lot. How crazy it is to predict very well described movement of the ball until long future without including the influence of others balls, particles or events. And that there are plenty of other more or less describable events in the world.
When it comes to predictions for the distant future or estimates for the very distant past, this is a problem, not only in the peculiar world of wave (quantum) mechanics but also in the world of classical mechanics – see a following example
The motion of comets and even planets is a chaotic motion, see the chaotic fluctuations of the orbits of Earth and Mars due to their precession. A similar situation occurs with Mercury, Venus and Jupiter. In other words, there is chaotic motion in the solar system, but for us on a long-term scale, as opposed to our short-term observations (hundreds of years). This chaotic motion in the solar system does not allow us to predict its evolution over tens or hundreds of millions of years, so the behavior of the universe on a macro scale cannot be predicted at all. And the oppposite to determine the distant past.
But let’s go back to the countability of different forms or events.
W
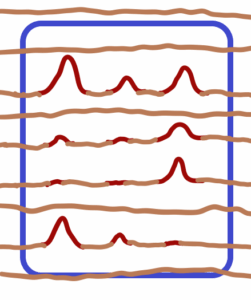
In the upper closed (blue) set – there are 3 x 4 = 12 elements (dark red), or points, or distingushable appearances in the omnipresent (light red) matter field. These appearances reperesent points. It is very difficult to decide which “points” to count and which not to count. Are there only 12 points or only 10 points? And maybe in a little while there will be 16 points or otherwise, when previously unsuspected appearances show up. It is impossible to isolate omnipresent matter field.
If we are able to count results of a creativity desire (intention) then we are invited to feel and value the intensity of the creating desire (intention) in relation to the given surrounding conditions.
How to count objects before they are created. How to count, how to calculate the intensity of the desire to create something – e.g. to create a pot or a music song? Objects can only be counted after they are created. The question remains the transition state – from idea to implementation and successful testing. When to start thinking about practical application. The power of faith, experience, determination? Hard to evaluate this mathematically. And that’s the point! What is needed here is personal experience, not the experience of others, but personal own (sometimes painful) experience, which of course reveals fantastic possibilities.
How many different curves can there be in the world. How to determine the degree of their differentiation. What will be the standard of difference. Who is going to judge?
How many mathematical coursess can there be, describable, compressible courses like y=f(x), where y is a dependent variable that depends by a functional prescription f(x) on the independent variable x. See sin(x), tg(x), log(x), … , sin(2x) + log(3x), … , etc. Are there more indescribable courses than mathematically describable ones, perhaps by the most complicated rules? And what about the complexity of the prescription? Wouldn’t it be better to give a table of values for y and x in a given interval?
See the laws of physics or the mathematical theory of sets using the concept of a set as a well-defined differentiable objects. See a pottery – the pot is or the pot is not. A moment ago the pot was not, now it is, and after a while it will not be again. It is the same in biology, in the beginning there is no apple, after a while there is an germ, then a growing apple, then a fully grown apple, and finally there is no apple again.
Generalized – in the beginning there is nothing, virtually chaotic quantum foam, which looks like nothing, after a while a part of the quantum foam inflates like a balloon and further expands and inside the expanding universe are created particles, stars, chemical elements, minerals and rocks, also the Earth is created with all apples, organisms and humans, who want to know the meaning of life.
To realize this in the world – there must be for some time worldly fixed forms and structures incl. processes among them. Shapes, structures and objects must be stabilized for some time – so called unchanging or quasichanging shapes and structures – see the evolution of biological species throughout the history of the Earth. There were no apples in the primordials. But there were trilobites, graptolites, etc. But I don’t see them around anymore. Sorry, I can see them, but only their fossils.
How to count the conceptual (existing only in potter´s mind) designs of the pots or pots that are not yet finished or those that are on the potter’s wheel or those that are being broken? And this is the way with everything in nature.
It´s not enough to count visible or perceptible or observable things and elements in the world but incomparably more is the ability (the experience) to create perceptible and observable things and processes like inventions, artworks, music songs, technical solutions etc.
Then comes mathematics (science at all), which needs differentiable structures, shapes – elements of sets. In simply words, first we need to have pots and then we can count them or create volume dependence on the diameter of the pots and much more.
In short, mathematics is useful for describing and classifying visible, perceptible, distinguishable structures. It is good to be familiar with the limits of mathematics. Mathematics cannot express what arises, what the unexpected arises. This is a surprise even for mathematicians. Certainly after a new object arises, mathematicians can describe its characteristics and classify the newly arisen object into the existing classification of objects. Further, mathematicians (mathematics alone cannot do this) can determine the object’s future evolution with some degree of probability based on observations of the object’s changes. But that’s all. Mathematics is not almighty. It doesn’t create new, it doesn’t destroy old, it just observes, describes and predicts.
In other words – to practice mathematics requires a stable distinguishable shapes, structures, processes and changes among them in the world for some time.
How to describe changes in shapes and structures? The described shapes and structures must be stable for some time. See counting in mathematics 1+1=2 or 2+3=5. For this we need stability and distinguishability of structures. E.g. biological species. A ladybird is a ladybird for as long as it is. So we have time to describe it. And if we don’t, another ladybird is born, and it goes on like this for thousands of years. But trilobites, for example, have been on the earth for about a hundred million years, but they’re no more. The same story will be valid for the appearance of ladybirds in the world. But let us cheer ourselves up with the thought that instead of ladybirds there will be another species of beetle, which our descendants will again have time to describe.
Back to descriptions of shapes and structures. We know that these must not change so often before we can describe them. In other words, shapes must not change faster than our ability to describe them. There is a slip between the change of the described shape and the change of the describer (usually a human, sometimes an automat). Description of slow changes by other faster changes. Both change, but the described changes are slower than the describing changes. If there were no noticeable difference, it would be impossible to describe.
What is the purpose of this? The purpose is to have growing experience through our perception of what is happening around us and why it’s happening. For which mathematics is the best tool. In short, to stimulate our senses with the use of mathematics. Mathematics cannot replace our way of learning knowledge and experience.
Mathematics, like computers, is the best and most wonderful tool ever created for learning about the real world. There is no better helper, no better tool than mathematics together with computers. But on the other hand, there is no worse master than mathematics with computers. A good servant, the best servant, but the worst master. The master was, is and should remain a human being.
See the mathematics part – combinatorics is closely linked to the number and distribution of otherwise indistinguishable points. As a substitute for indistinguishable points, we can mention electrons, we also cannot differentiate between them. More points or electrons does not mean that all possibilities could be realized. See the entropy from 2nd law of thermodynamics. There must be some initial differences in energy levels.
Whatever originated in the world can’t be divided into exactly the same parts. Whatever came into being is the original, whatever structure is unique. Unique is a whole that includes all subsets, each of which is unique. It is not possible to construct two equal segments and then connect them at exactly twice the length and it is equally impossible to split one segment into two equal halves. Splitting the continuum requires irrationality.
The equation 1 + 1 = 2 has no meaning in the real world. There are no the same shapes, structures, elements, subjects or anything else. Yes, we use this equation like model. But we must know this is only the model, our approximation.
In the same way we could pretend the ideal straight line if we see a very fine piece of polished metal surface. The same with the ideal ball if we see very pretty polished balls into gears. If we go closer then we see something like mountainous landscape – surface roughness profile that vibrates in response to the thermal movement of molecules and atoms. If we go more closer then we are able to see foggy appearance of particles as excitations of quantum field.
See also long-distance action. There has to be physical contact of the bodies. That’s why once upon a time centuries ago gravity was hard to understand, and later electrical and magnetic forces. How it is possible to act through empty space without direct physical contact of the bodies. Much later, we recognized that the contact of the bodies itself also took place at a distance — Pauli’s exclusion principle applicable to electrons in atomic shells. When we take a closer look at the contact of the bodies, we see only and only the deformation of the electromagnetic fields of atomic shells. Like approaching two magnets with the same pole facing each other.
How to distinguish random events? How to distinguish a random number series from a non-random number series? After all, each number series is different from the other if they are not identical. We have to establish some kind of regularity. Something that repeats despite the chaotic background. Something that has a pattern relative to the length of the number series. So it also depends on the length of the number series. Who’s selecting what to distinguish? Man or machine?
Visibly distinguishable, perceptually distinguishable patterns. How in random states or events to start with distinguishability. But after all, all random events are distinguishable – one from the other. But the frequency of occurrence of distinguishable features gives a straight line – there is no preferred state, shape or process. Randomness cannot be determined in this way, however, a regular series with a clear regularity will have an equally frequent occurrence of its elements. Thus, testing for randomness consists in using higher perception, in finding order. Meaningful order (the question is what is meaningful). No matter where we observe, there is randomness everywhere – unpredictability. Everywhere? But even random events (chaos) need a framework, a limitation.
How to distinguish the indistinguishable, the originally invisible, if we do not want to distinguish the distinguishable with honesty.
See musical compositions – series of musical notes (cdefgahc) – write down a composition (or part of a composition) in numerical series and evaluate the randomness, usually there are repetitions, but there can be compositions numerically random but still beautiful. See coding with random numbers – we must have a series of random numbers. So add randomness to a piece of music?
Mathematics is the result of differentiation. Mathematics is compressible. But nature is not compressible. However, from a single quantum, or even deeper, from nothingness, the entire universe can arise, with all its different, distinguishable structures. But even so, mathematics cannot yet come into being. For each structure is different, distinguished from one another. they have no common denominator, no similarity to one another. Everything would be 1, 1, 1, 1, … etc. So the necessary next condition is the appearance of self-similar structures. See elementary particles, elements or biological species. Each individual may be an unrepeatable original, but they have a common denominator, a basic characteristic. They are grouped into sets. With sets the language began to exist – to name sets. After that mathematics come into being. The common denominator abstracts to an ideal form. In other words, everything that looks like a circle is idealized into an ideal circle. Even though every real circle is different from each other. And it does so within a given interval – say, with respect to the basic building blocks. How to distinguish a circle from an ellipse? Where does a circle end and an ellipse begin? Does it make sense to ask this question? Rather, ask why self-similar structures exist in nature in an ocean of chaotic structures.
Even more differently, mathematics is a subset of the real world. Not all continuous functions are differentiable. And not all beautiful shapes are mathematically describable. Mathematics has no chance at all in describing, let alone predicting, random, unpredictable structures.
The law of inertia for material bodies through the history
a brief recapitulation:
Aristotle – limited motion of bodies
Newton – unlimited motion of bodies
Einstein – „limited“ motion of bodies in spacetime
The history of extrapolation. Extrapolation from observations of natural processes at a given level of natural processes.
Newton’s first law: A matter body remains at rest or in motion at constant linear velocity unless an external force acts on it.
The law of Inertia. The result of the first law of motion is an escape velocity: Every body accelerated to the escape velocity will move away until infinity.
According to physical textbooks, the Newton first law of motion is an brilliant extrapolation of our experience.
Every body remains at rest or in straight line motion unless it is caused to change its state by external forces. In the real world, where there are always some forces (resistive, frictional, … , gravitational), the body will stop after some time or will stop at infinity in the case of an escape velocity. In other words, the so-called ideal case is not possible in the world. It is possible to reduce the forces resisting motion, but not to cancel them. However, even in the so-called ideal state, the definition (without external forces) is meaningless. There is an contradiction in the case of the ideal state. The misunderstanding is at the very beginning – the level of observable natural processes.
It follows from the very nature of a material body – for wherever there is a body or bodies, there are always external forces (gravity – deformation of spacetime). There is no possible state of having material bodies without external forces. The external (gravitational) forces are the results of the deformation of spacetime and they are related to every material body.
As we know today, bodies are only in the universe along with time and space. There are also forces interacting with each other body as the result of space and time – see gravitational force. For there is no space or time without matter and vice versa. There is no matter, no body without space and time.
And so the meaning of the Newton 1st law of motion in the light of space-time bound to matter (bodies) does not make sense also for so-called the ideal state. There will always be a gravitational force acting on a body, e.g. in intergalactic space, and such force always influences the body. The material body itself is an indivisible part of space and time. The material body as we perceive and measure it is an excitation of the omnipresent quantum field.
Thus the ideal state without all acceleration no forces would act on the body, is impossible. The nature of the contradiction is in the very beginning. That it is a body. If it’s not a body, that’s different. But we don’t know and can’t describe the motions of non-bodies. Where there are bodies, there is always force action and the impossibility of movement without limits. It follows necessarily from the nature of bodies. Even if there is one single body, it will necessarily gravitationally affect itself in motion.
There always be forces among bodies. Yes, in a case of an escape velocity, there is no chance to stop accellerated body, but such body will be still influenced by gravitational field of the first body and, no doubt, self-gravitational field.
There is another point of view. The body is the source of a gravity force. Such force curves the spacetime.
Bodies, by the very nature of bodies, cannot move freely through spacetime without forces.
There is an equation – the body means gravitational forces and gravitational forces mean the body or bodies. Without bodies there are no gravitational forces and vice verse. Without gravitational forces there are no bodies, either.
Let’s imagine a thought experiment – there are only two bodies in the universe, that have been accelerated to escape velocity from each other – so they will move away to infinity, as we calculated from the equations of classical mechanics.
But the reality in light of Einstein’s equations of general relativity is different – see the following
Two bodies accelerated from each other to the level of the escape velocity do not mowe away until infinity, but these two bodies will deform spacetime. The conclusion – these two bodies with escape velocity do not move away, but they will follow the main curve of spacetime. In an ideal state the main curve will be the main circle of an sphere. The result – two accelerated bodies will meet after a long time. The time is given by (growing) mass of two bodies and their escape velocity from each other.
This is not a negation of Newton’s law, but a specification of it by knowledge that Newton did not have in his time. In other words – every model, every theory, is valid for a certain range of natural processes, and it is impossible to establish a universal formula. Especially if we don´t know every process in Nature, plus every process is unique – there are only common characteristic – like appearance of hexagons in snowflakes.
The age-old human tempation of applying abstract models or ideas from a given level of natural processes to the whole of nature or the universe and then being surprised that nature or the universe does not work according to them.
However, models are good, proven models. Yes, they are good and repeatedly tested, but at a given level, at a given scale of natural processes. Moreover, a model is a model – i.e. a simplified, abstracted description – so it has limited validity even at the original level from which the model was created.
Go back to bodies:
The bodies have to be together in spacetime (spacetimematter). There is no chance for matter bodies to escape from each other to infinity. There is an exception if there is external force (power) above all bodies. Sometimes called dark energy.
Conclusion:
The greater the mass of the bodies and the greater their escape velocity, the greater the deformation of spacetime and the smaller the radius of the main circle and the shorter the time for the bodies to meet. And vice versa – the smaller the mass of the bodies and the smaller their escape velocity, the smaller the deformation of spacetime and the longer the time it takes for the bodies to meet. See an image below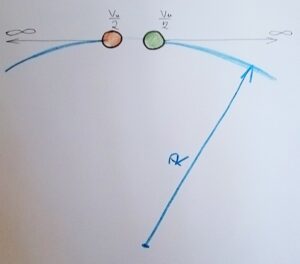
In a rough analogy, it is like sailors on two ships in an earthly ocean, drifting apart into “infinity” until they meet on the other side of the globe.
Even light cannot leave this spacetime (spacetimefield). Just as light cannot leave our universe. Light (electromagnetic waves) is given by the properties of spacetime. It doesn’t matter if we call such spacetime the elementary quantum field or the ether.
Go back to simple mathematics. We have a base coordinate system. E.g. Polar coordinate system – there is a central point with N lines passing through it and circles around it. This coordinate system still looks the same whether we scale it up or down. To know the scale – we need to introduce another point. See below
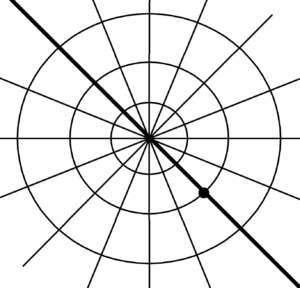
And only now do we have the basis of the polar coordinate system. This basis is a clearly given by line (meridian) that passes through the two points that mark the section – the base unit for length, position and direction. This next point must defined properly. In relation to the observed surrounding reality. Only infinitesimal distance dL is not enough.
It is impossible to describe the processes inside one point (zero size) using the derived units from the existence of another point and the space between – the base distance. Then we can get into contradictions. See the singularity of the universe, the so-called black holes or the singularity of the Earth’s poles. In the case of the poles, the situation is simple. If we are standing on a pole, it is hard to give a direction to go. Surely it is enough to give the meridian, but it is indistinguishable at the pole. So we have to move aside far enough to distinguish which way to go. So here the resolution of two points – the point of the present position and the point of the pole (north or south pole) – is what matters.
to be continued …
Let’s go on with the simple mathematics – especially the much quoted Gaussian density function. See below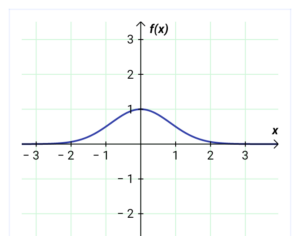
Such function is given by a very simple formula y = f(x), see below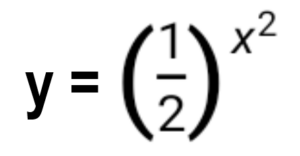
where instead of e (base of natural logarithms) is the number 2
There are infinite possibilities how to modify this function into very interesting waveforms – See the waveform of a wave packet – e.g. a photon. See below
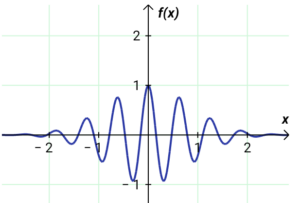
The frequency has a sinusoidal shape. But the ” bound” sinusoid has the shape of a probability Gaussian curve of a normal frequency distribution. The sine wave is modulated by the Gaussian course. The result – the “bound” frequency of appearance of a particle – wave particle – wave packet.
See curves below – dependence of the probability density on the distance from the nucleus of the hydrogen atom.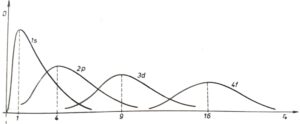
There are clearly visible peaks of courses that determine the wavelength of the emitted radiation. But we also see that the peaks are not discrete, but continuous. They are an integral part of the courses. In other words – the wavelength of the emitted radiation (when the electron jumps) changes.
Go on. Imagine a continuous and smooth line. See Fig. below
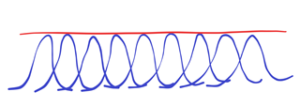
This line is not necessarily smooth and continuous when we “look” at it more closely. This line may consist of many probability appearances – see vacuum field excitation from so-called quantum foam anything can be created. See next Fig. below
We can count the peaks with some resolving power. Count the peaks of given course. Courses or functions of the probability density of vacuum excitations. However, these courses with their peaks must be stabilized for some time. Stabilization may consist in the regular renewal of the courses with their peaks.
Mathematics cannot explain Reality, Nature in its diversity. However, mathematics is a product of abstract thinking – a simplification of observed processes. These processes, even if they last for a certain period of time, can disappear or be influenced by other processes of which we have no idea.
Maths is a product of grouped random events, not their source.
Let’s imagine two series of numbers. One series is predictable numbers – e.g. x+1 or the function sin(x) or log(x) etc. The other series of numbers are numbers that are unpredictable, i.e. random. It is impossible to find any pattern of their repetition. Now let’s do the sum of these two series. What do we get?
‘1, 2, 3, 4, 5, … , etc. and 0.237, 0.986, 0.011, 0.455, 0.671, … , etc
After summing the two series, we get a new series
1.237, 2.986, 3.011, 4.455, 5.671, … , etc.
The integers retain their pattern, but their decimal progression is random. The situation changes when we add the numbers in the third decimal place to the random numbers.
0.001, 0.002, 0.003, 0.004, 0.005, … , etc. and 0.237, 0.986, 0.011, 0.455, 0.671, … , etc
After summing the two series, we get a new series
1.238, 2.988, 3.014, 4.459, 5.676, … , etc. How to extract the originally added numbers with simple progression 0.001, 0.002, 0.003, … , etc. We will not be able to distinguish the added numbers – their predictable progression. In other words – we get a purely random series again. It is impossible to extract from such random series any meaningful series back, or we can fabricate any series we wish. The real predictable series completely dissipate in a mix of random numbers, unless we know the predictable series or the random number series. And here we are at entropy. Anyway, this is the principle of an unbreakable cipher with encryption using a series of random numbers. The advantage of a cipher is unbreakability. Disadvantage of the cipher – to transmit a series of random numbers to each other and not to repeatedly use this series.
Go on. Let’s imagine again two relative series of numbers. One remains, the integers from 1, 2, 3, … , etc. The other series will be random numbers with variable values, or with different positions of the decimal point.
1, 2, 3, 4, 5, … , etc. and 0.237, 9.860, 0.011, 45.500, 0.671 … , etc
After summing the two series, we get a new series
1.237, 11.986, 3.011, 49.500, 5.671 , … , etc. We can see at a first sight that every second number, or its integer part, is an odd number. Now imagine that a series of random numbers contains a randomly changing position of the decimal point. In short, after adding the two series, we get longer or shorter series where we determine the added numbers with a series where we are unable to determine added numbers.
And that brings us to the noise. Noise that influences the transmitted signal. As well as the noise of chaotic events that will influence our abstract models in the future, or vice versa, how certain we can be of what’s happened in the past.
Every theory, every model is valid in some range – see an upper image. The more general the theory the greater the range of validity with little accurate results. The more detailed the theory the narrower the range of validity with very accurate results.
The propagation speed of waves in different environments . Without fluctuations no propagation speed at all, no movement, no changes, no development. Imagine a point like expression of the peak of the waveform. The point itself means nothing. We don’t know whether it represents the peak of the sharp waveform or the peak of the sloppy waveform. Which is very important in real applications. See below
Thera are 5 points. The point has variable power – from 1 to 5. The power of point means its sharpness or rapid progression in given range. The smaller range with rapid progression the more energy and vice versa. See also wavelenghts or frequency. If there are more connected progressions together then we obtain the “pretty” function. See below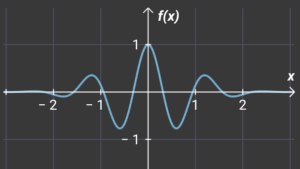
This “course” has low energy the we introduce next “course” with greater energy. See below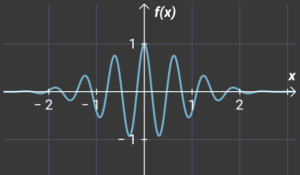
If we want to imagine more and more energetic “wavecourse” then See below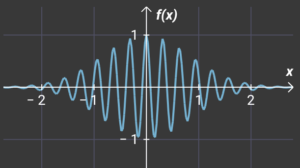
And in this way we can go on and on in shortening the wavelength. You could say up to infinity – but only ideally, because in our universe, the wavelength of the particle would represent an energy greater than the entire universe. See below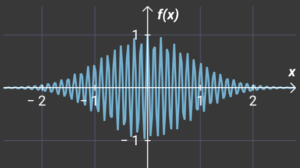
From the above it can be seen that the shorter the wavelength (higher frequency) the greater the accuracy, but also the greater the influence of other processes. And vice versa, the smaller the wavelength (lower frequency) the lower the accuracy, but with minimal influence on the observed processes.
Imagine a number series of random numbers. A series without end. As the series progresses, we can discover certain patterns. Not just an ordered sequence of numbers, but perhaps functional relationship. See following number series
…..804854251355393280854916365179028116820495388064589809751234321012343210190812402118072221120937557584523297371065…..
There is a clearly identifiable pattern in the series – red marked. This random series, with a little imagination, represents random fluctuations of the quantum field. The fluctuations are completely random, unpredictable and they are called zero vacuum fluctuations. In such an environment there are excited states of the probability of the appearance of e.g. an electron in an atomic shell. Is there another fundamental question? How to distinguish random structures from non-random ones? Or how does one non-random structure in a chaotic ocean distinguish other non-random structures? For there is no outside observer. How to measure the degree of randomness or the degree of order? Use the selected standard non-random structure? On the one hand, tight order, on the other hand, randomness of chaos.
See next random numbers series below
…….59528890163938123332114194511344217155134146095204761012343214612343222274101234320715686828980012343213189412243210186055872687666887359546223433138123432195216864838………
We see groups of ordered numbers 1234321 that occur repeatedly. Let’s look closer and we see that our ordered numbers contain changes in them. For example, instead of 1234321, we see 1224321, etc.
Waves or particles? Hardly to write. There is always different situation. Foggy blurred background of quantum field. A foggy blurred background from which appear and disappear and are renewed wave-particle shapes. Always different – an indefinable grouped of chaotic events into shapes and structures that appear to us as continuous. We have a limited experience that confuses us – shapes, spheres …. but we too are given by grouped chaotic events. But we have perception.
Yes, when we look closely to the structures and shapes we recognize indefinable, indescribable chaotic events that are grouped into familier forms, shapes – appearances of particles, these further into atoms, molecules, minerals up to living organisms.
All these grouped events into shapes and structures are always different, indefinable in their details. Sure, there is an abstract framework, but even that is subject to changes. Either internal changes or external ones.
Lawfulness, regularity or periodicity in a set of data is more likely to be found by those people who expect it and know how to look for it, while the most precise observational data alone does not lead to a deeper understanding.
But periodicity or regularities are not perfect, better said, they are not eternal – in short, they are valid for a limited time. Even if they are valid for a very long time, like the orbit of the planets around the sun, that does not mean that the stability of the orbits of the planets will be the same for millions of years to come. There are other laws – like the motion of comets or nuclear forces – that can unexpectedly disrupt the stability of planetary orbits. Not to mention the basic fact that all periodicities and regularities are “grafted” onto a purely chaotic environment. Thus, the most precisely measured “constant” slightly change in the “rhythm” of vacuum fluctuations . So what is the point? Is it about observation or is it about abstract thinking? It is both! To learn how to abstract what is significant at a given time, at the current time. And at the same time to know the general regularities (laws) that can affect the most stable natural processes. That is, not only to think, but to give place to other observations – perhaps in the field of comets or nuclear forces. All this is called Experience, fine and firm (decisive) perception.
Another way of looking at the random series. This time in graphical form. How to estimate the source of a line or curve? Better written – what are the curves that make up the resulting line or curve? See below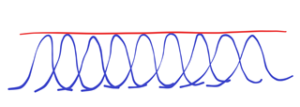
But a straight line can turn into a curve with a different course. See below
The upper picture is closely related to the resolving power – how to distinguish marked differences in the course (red marked)
Also there is a big difference with a course of nearly ideal lines. It depends on what they consist of, whether high frequencies, mid frequencies or low frequencies. See below![]()
The straight line is still the same, but the frequencies of which it is the envelope change significantly. From the highest frequency, through the middle to the low frequencies. We could write that in different parts the straight line has different “weight” – different energy (energy content).

See uppper image – there is a course of Continuity – unexpressible course, it is impossible to make a formula, to mathematically describe that course in its wholle. Yes, we can more or less precisely to desribe parts of that course, but only parts and it is impossible to predict the future course or to estimate passed course. Remember the number series mentioned above with frame regularities. But such regularities appears to be regularly – they appear regular but in fact this is the result of our simplification in current state.
We can verify by observation only current state.
Media density versus wave propagation speed. Transmission of waves through two different media. Here the angle of incidence is important.
Try to solve ideal Euclidean geometry especially the fifth postulate, where it says that a parallel line (marked orange) can be drawn through the point P that is situated next to a line. See below
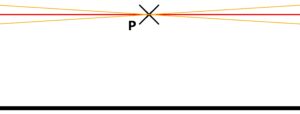
That´s true. But the full text of Euclid’s fifth postulate is that only one parallel can be drawn. And Euclid wasn’t able to prove that. Lobachevsky assumed that tere were two positions represented by the angle A (marked yellow), that all lines inside that angle are not parallel to the ideal line. These lines will never meet the black line, no matter how far they are extended. Imagine next situation – illustrated below
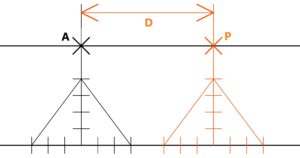
There are also one line, the ideal line from infinity to infinity with two given external points A, P at the same ideal distance from the line. These given points A, P have the distance D between them. It is clear that only one parallel will pass through these two points. Imagine the following process – the distance D will gradually approach zero. It will be interesting to see what happens near the point P.
To solve the area of a circle. To solve it by using squares. The area of the circle Ac with a radius R is approx. equal 3 x (R x R). See below
The difference between 3R and real Ac is cca 0,14… Quite sufficient for rough calculations and estimates. Really, the ratio between the circumference O and radius R of the circle is always a fixed value, regardless of the size of the radius, the circumference O is always equal to π (3.14) times the radius R., then π = O/R. As in physics, there is a constant ratio h (6,626 x 10⁻³⁴ J/s) between the energy value E (J) and the frequency f (1/s) of the emitted radiation. At any given frequency, the Energy E of the radiation is always equal to a given value of frequency f, then h = E/f.
There is a next interesting fact with the angle in the circle. The base angle is expressed by Radian in the unit circle (R=1). See below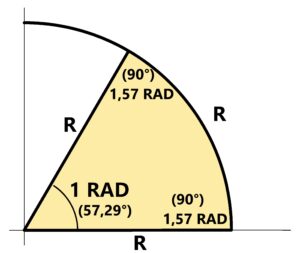
1 Radian (RAD) is given by the angle φ where all sides are equal to R (radius of the circle). One of three sides is the arc. The sum of these three angles of such peculiar area is equal to 1 RAD + π (3.14). The angle φ = 1 RAD means that all sides are equal, which implies that a given opposite arc always has the length Lc of the radius R of the circle. Then Lc = φ * R. We can easily solve the arc of the circle. For φ = 2π we obtain Lc = 2π * R = 0 the full circumference of the circle. Angular velocity Ω = φ/t if φ = 2π then Ω = 2π/t where 2π means one round n over the entire circumference of the circle. There could be more n rounds per second, then n = 1/t. Then Ω = 2π * n. To solve circumferential velocity or acceleration is very easy with using radians. Then circumferential velocity V = 2π * R* 1/t = 2π * R* n = Ω *R.
Mathematics (Abstraction) is the best helper that can be for research, analysis of natural processes. But it is important to remember (and not forget) where mathematics came from, what its origins are. In short: mathematics originated from a stretched space containing different shapes, forms, and events that had been stable for some time. It was only through abstraction that the peak of the stabilized shape was transformed in the mind of the mathematician into an ideal point with zero size. Similarly, in the same way the distance between two peaks of stabilized shapes was transformed into a segment. Furthermore, by extending the segment to infinity, infinity was created, without any changes, shapes, or other disturbances. It is good to realize that these results of the abstract mathematical mind do not exist in nature (space-time) and never will. However, they are a tremendously helpful tool in the analysis and study of natural and social sciences, and mathematics is indispensable for further development in technology and crafts. See, for example, the important definition of function continuity. This definition makes it possible to solve distinguishable shapes at different levels, from microscopic to macroscopic states. But solving the de facto unsolvable is a problem that brings more problems than benefits, see the definition of ideal distance using an ideal point with zero size. In other words, trying to express something using nothing. This leads to such paradoxical constructions and considerations that the beauty of mathematics is lost. See also the equal number of points between a square and a section (G. Cantor – infinite sets). Yes that´s right for ideal circumstances but in practice – especially combinations, how many ways to arrange e.g. a square image – how many combinations, how many different images we get. And the same is true for a limited section on the ideal line. However, the possibilities of mutual (geometric) arrangement is different between the square and the section even if the same number of ideal points. Not to mention that people perceive the continuity of shapes through their senses as a shell of insignificant details—see surface roughness. But sometimes, details that were originally insignificant can take on significant importance—see rupture in mechanics as a result of material failure. And we cannot do without mathematics in mechanics.
For mathematics cannot exist without an expanded space with different shapes, distinguishable and stabilized for some time. Mathematics is an abstract product of spacetime and not its originator. Like language is a product of the human mind for naming of natural forms and processes and not their originator.
A beautiful example is the postcard – how to study it, to explore it. Here we are not studying details, but the whole, Mutuality. What do we see under the microscope? Random colored groupings of dots. And if we magnify even more, just a mishmash of different coloured fibres. It’s the same with our world – what do we see when we magnify it x times? Chaos. What do we see when we zoom out into intergalactic space? Chaos again.
We have an area. The area in its size varies gently through hundreds of hours. The change is, for example, a few tenths of a percent of the area. What is the point of measuring such given area to the nearest tenth (or hundredth) of a percent? Perhaps just to make sure that more detailed measurements are meaningless. For one thing, accurate measurement takes a long time and, above all, the area changes by a given accuracy of the measurement.
And so we come to the experience of a quick estimate within tens of percent, or a more detailed estimate within a few percent (see square grid, etc.). On the one hand, we are quickly oriented, and in a more detailed or detailed analysis we know what the limits of the resulting solution are, and so avoid fatal errors due to over-detailed analys in the case of very detailed equations and procedures. After all, all formulas in physics, mechanics, thermodynamics are only “framework” formulas with a certain accuracy for given processes. Let’s take a geometric example. We can easily calculate the areas of triangles, squares, rectangles, and other basic geometric shapes. But what if we have an area that is indefinable? See below

How to estimate the area of the upper illustrated shape? Very easy. Just fill the rectangle with the given area, just by eye. Because we have a well-trained sense of proportion in our “eye.” See below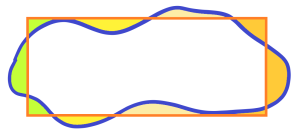
We are able to interpolate the given indescribable area(s) into rectangle(s) as best as our experienced “eye” allows. In the upper image, we can see how the shapes in the measuring rectangle roughly balance out with those not included. Calculating the area of the rectangle is now easy. Yes, the result is not so accurate. But for a first approximation, it is prompt and, above all, the result provides a clear framework. The result has a big advantage – to give the interval where the most accurate result has its place. Then there will be no shameful situations where details are measured as accurately as possible using an iterative method or other procedure, while the basis is neglected by hundreds of percent. I remember the very shameful situation, where the spring hangers of the high-energy pipeline were “carefully” measured, but the pipeline was 1 m longer compared to the model, which meant a greater load of several hundred kilograms, so the “careful” ones missed that. Of course, I have nothing against accuracy, against the most accurate calculations possible, if they are necessary. But first, a framework must be established and then refined as necessary.
There is a big temptation in our “eye” evaluation (or surveying). When it’s by eye, we’ll take it roughly. Quite the opposite! When it’s by eye, we’ll try to balance the proportions as best as we can – rectangle versus undefined area. And after some time of “training” our “estimation” experience will improve. And then there will be another temptation. That our growing estimation and trained “eye” will adequate.
to be continued ….
See below – there are articels on the subject of this section. If you want, download the pdf file.
See below – there are unsorted brief remarks waiting for word processing to articels
