Considerations on the subject of chaos. Not so much the order arising from chaos but the existed order in spite of surrounding chaos.
A few phrases at the beginning
…in the beginning was chaos …. from chaos arose order ….. or chaos is the basis for the principle of self-organization which explains the present universe with its complex structures … etc.
Very interesting question – the existence of order in a chaotic environment. Order in chaos, stabilization of forms and events in a chaotic environment – See the arrangement of crystals or the beauty of flowers
How to define the chaos? For one thing, we need something for the chaos. Forms associated with events. The chaos is a process with random behaviour of distinguishable forms. These forms are indescriabable. Always different to each other. The forms differ from each other, even if only slightly, but they still differ – to infinity. From mathematics we know that between two points, slightly apart, we can place an infinity of next different points.
What is the origin of chaos? E.g. for so-called self-organization theory. How does chaos self-organize?
Self-organization theory – the reciprocal movements of a complex system controlled by the laws of non-equilibrium thermodynamics. According to this theory, the system can “spontaneously” organize itself if energy flows through it. In other words, if we have energy differences and a chaotic system among them, and we start the energy flow given by energy differences, then the initially chaotic system will start to organize itself into higher orderly predictive complex structures. This is verified many times not only in thermodynamics, physics, but also in chemistry or biology. The proven theory in practice many times. But it adds more questions to the origins of life and the origins of the universe than it explains them. On the one hand, the requirement of an energy differences. Secondly, an impulse triggering the flow of energy. Furthermore, the regulation of the flow of energy and, above all, the origin of energy, or what we call energy.
It is very unpleasant to expect chaos to infinity. See an image below

Chaos everywhere. It doesn’t matter if the chaos of thermal or vacuum fluctuations. There is a contradiction. But what is valid for a finite, however large, number of particles and boundary conditions may not be valid for an infinite number of particles. Especially for indefinable fluctuations of the quantum field. There are already contradictions in chaos that do not cancel out in its application to the infinite, infinite expanse of chaotic behavior – fluctuations, gas molecules, etc. Chaos, chaotic fluctuations cannot be stable, they must move, or they must arise and disappear, there must be mutual collisions, mutual interaction. This is a question of further research, or considerations based on detailed observations on the basis of derived base units. Not to mention the necessary and unquestionable existence of at least two different chaotic environments – the basis of thermodynamics.
The question of what is beyond chaos is meaningless. It doesn’t make sense in the view of derived units from regular appearances modulated on chaotic fluctuations. Just like asking what’s outside the universe. The universe and its internal parts, including the chosen units, behave as they do. There is no external observer, only internal observers with internal relationships. The question of the outside is not a matter of science, but a matter of Faith – and that is another topic.
What is the meaning of chaos? How can chaos exist? Where did chaos come from?
Chaos can´t exist by itself, by its inner power, by its nature. It can´t hold together by its own properties. Chaos cannot sustain itself in chaotic behavior. Chaos must be sustained, allowed to behave chaotically. Firstly – to be in motion and secondly to be limited from the outside or inside. Without allowed motion and limiting conditions, the chaotic particles (waves) would collapse in themselves. Or they would have drifted apart indefinitely. Very roughly – See particles of gas. These particles must be in motion and to be limited in closed space or limited by gravitational field. The gas molecules would either collapse into each other or move away from each other.
The gas is defined as the collection of particles (waves) as such exists only in closed space or with gravity forces. Without gravity forces or without closed space there is no gas as we understand it – colliding particles. To stretch the space infinitely – there are no collisions, no gas, no random fluctuations, no chaotic behaviour. Chaos without collisions is not the chaos. Collisions are given by external forces – gravity or closed space like vessels or anything else. We quietly postulate this, but it’s important to think about it in more detail.
Without a closed space or gravity forces, there is not only no gas, but there is no chance to condense into a liquid or solidify into a solid. See phase transitions.
Chaotic behaviour needs bounds. Chaos needs boundary conditions. Without bonds, without boundary conditions there is no chaos, no chaotic behaviour.
Two conditions defined the chaotic behaviour of gas
1) the limited space
2) the motion of parts.
The gas need limits – without limits gas could not exist There must be limits for interaction – reciprocal collisions among particles of gas.
It is very difficult, if not impossible, to apply partial knowledge of the classical behaviour of gases to an unlimited number of particles, waves or various fluctuations.
Let´s start with the origin of chaotic environment. E.g. the balls in closed box. Let´s start with one ball in close box. See below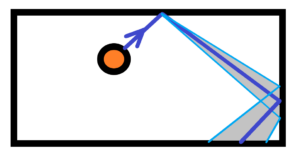
In the beginning there is the ball with initial velocity. The ball is bounced off the wall of the box. But the bounce will have an angular tolerance. See grey filled area. We can predict the maximum number N of bounces based on a mathematical model. And that’s the point. The range of tolerance will increase with every bounce. And after a while, the angular tolerance will be 360 degrees. The mathematical model ends. Further calculations would be useless. The range of angular tolerance is influenced by the shape and texture of the ball, the course of its stiffness, the properties of the box wall, etc.
The more balls inside the closed box the shorter the transition time to chaotic behavior. But it depends on the diameter (size) of the balls relative to the size of the enclosed box. The smaller the size of the balls relative to the box, the longer the time it takes to transition to chaotic behaviour. How to determine the transition time? There are variable inputs: Size or volume of box, size or diameter of balls, the number of balls, the regularity of balls and the regularity of box, the regularity of mechanical properties of balls and the enclosed box, the temperature of balls and the enclosed box, surface roughness, etc. Is there any sense in analyzing and solving all this inputs? The fundamental parameters are the ratio of the size of the balls relative to the box and their relative velocity, together with the experimentally measured angular tolerance when the ball bounces off the wall and between the balls relative to each other.
The result is the time of transition of the balls into chaotic behavior. The transition time is determined also by the quality of the balls and the box – their regular shapes, mechanical properties together with the quality of the material from which they are made and also by their temperature. And also our measurement – or rather its accuracy. Even if we are the most accurate in our measurements, we will not get any further. The higher the temperature, the higher the fluctuations.
There will always be a transition to chaos. Even in the case of so-called ideal conditions – ideal spheres, ideal materials, ideal surfaces, ideal zero or equilibrium temperature together with ideal fluctuations – there will be a transition (extremely long time) to chaotic behaviour. This is because of the maximum possible mathematical accuracy – the number of decimal places.
Temporary conclusion: Does it make sense to make short-term predictions? It does. It is necessary to know what will happen in the near future and to verify the quality of the mathematical models. Does it make sense to make long-term predictions of ball behaviour? It doesn’t. Because in the end, it all dissolves into purely chaotic behaviour.
Replace the closed box with two horizontally spaced walls. The ball will bounce repeatedly between them See below
The measured position of the ball is in the middle. The direction to the right shows the future and the direction to the left shows the past. It is clear from the image that the position of the ball, or the uncertainty of its position, increases both to the right (future) and to the left (past). The degree of uncertainty depends on many conditions – the shape and quality of the ball and walls, their mechanical properties, etc.
There are three possibillities
1) in the past – everything is hidden in chaotic behaviour
2) in the future – everything is hidden in chaotic behaviour also
3) the actual state, with some uncertainty in the future or into the past
See thermodynamic – How to predict the path of a particle in a chaotic gas? What will be the quality of the prediction? Because the density of the gas, the density distribution of the particles, matters a lot. How crazy it is to predict very well described movement of the ball until long future without including the influence of others balls, particles or events. And that there are plenty of other more or less describable events in the world.
E.g. the motion of comets and even planets is a chaotic motion, see the chaotic fluctuations of the orbits of Earth and Mars due to their precession. A similar situation occurs with Mercury, Venus and Jupiter. In other words, there is chaotic motion in the solar system, but for us on a long-term scale, as opposed to our short-term observations (hundreds of years). This chaotic motion in the solar system does not allow us to predict its evolution over tens or hundreds of millions of years, so the behavior of the universe on a macro scale cannot be predicted at all. And the oppposite to determine the distant past.
Not to mentioned the top of science – the discovery of chaotic matter (quantum) field with its “zero” fluctuations that permeate the entire universe. As we know the chaotic behaviour is completely indescribable. In this chaotic ocean there are certain forms and processes with varying degrees of stability. This degree of stability varies over a great range, from the “stability” of protons, electrons and bound neutrons to the instability of free neutrons and many other elementary particles, as well as the stability of chemical compounds, minerals and organisms. These stable structures are subsequently describable. The extent of their description is determined by the degree of their stability.
The situation with the chaotic behaviour not only of the gas but also of the quantum fluctuations is similar to the probability calculus. Particles with no external limits would expand to infinity. Thus, there is no chance of at least two particles meeting. Likewise in probability – there must be limits (edges of the dice, sides of the coin, given possibilities, etc.). If there were no limits we cannot evaluate probability. It is hard to calculate the probability of one hard-to-differentiate event out of an infinity of possibilities of hard-to-differentiate events. However, we know that when we look more closely we discover still new details, and likewise when we go the other way, to a great distance – still new and different structures.
How to cancel chaotic behaviour? How to cancel gas properties? Very easy. Put the gas into closed box. After that let´s fly to intergalactic space. Open the box and all chaotic behaviour will be over. Gas will not exist from this moment. But each particles of the gas had some movement? The movement didn´t dissappear. The particles are free to move freely through space, each in the direction it had after leaving the box. At some distance from the box, the particles will occasionally collide, but at multiples of the distance from the box, each particle will fly to its own side without ever colliding with another particle. Until particles reach the nearest galaxy with their stars and planets.
On the other hand we can cancell the chaotic behaviour if we reduced the particle speed to zero then particles would collapse in themselves.
Go on! Imagine only particles in closed box in empty space (without galaxies) – imagine material particles of chaotic gas motion. Every particle has its own mass. Every particle weighs something. We will open the box and what will happen? The particles are free to move freely through space, each in the direction it had after leaving the box. But we are in the empty space without galaxies. In other words, the particles fly into free space and if their velocity is less than the escape velocity they collide again at the starting point. But the gas will no longer exist. The particles will be motionless together, at most oscillating due to internal atomic motions.
If their velocity is greater than the escape velocity, then the particles will move away to “infinity”. But we already know from inertia and spacetime that the slightest matter deforms spacetime. In short, the free particles will move for a long time through the gently deformed spacetime until they come together again at another place – after many orbits of the curves of the deformed spacetime.
Imagine our universe which is filled by moving particles. Every particle has its own mass. These particles interacts with each other by collisions among them. They are attracted to each other, but they will never be away from each other. The range of their appearance defines the dimension of the universe. It doesn’t have to be just particles, but perhaps the basic vacuum fluctuations of the quantum field.
Let’s try the following suggestion – in the beginning of the universe there was no chaos. In the beginning there were primordial origins of boundary conditions. The result of boundary conditions is the chaotic behaviour of everything inside the boundary conditions. Not mention wildly „bubbling“ quantum fluctuations.
It is impossible for ours (humans) to explain the subject of primordial origins of bounding conditions (gravity, closed space) by derived thermodynamical equations describing behaviour of bounded chaotic gas which depends on upper mentioned bounding conditions.
If the chaos can´t support itself then the chaos is unable to form itself to higher structures. Especially organized organism. The flow of energy through chaos doesn´t solve anything. See self-organization theory. We need chaos, resp. at least two different chaotic environments with the difference of an energy levels, after that there are some germs of organized structures.
Go back to thermodynamics – the well-known thermodynamic equation for the chaotic behaviour of an ideal gas for a given pressure, temperature and volume, the equation pV = nRT needs at least two different chaotic closed space with the ideal gas, it doesn´t matter if the closed space is the universe, the atmosphere of the Earth or closed vessel or a cylinder with a piston inside that.
For thermodynamics we need at least two different chaotic environments. One of which is closed. See a closed volume of gas in the atmosphere. Two differently chaotic environments in terms of the intensity of chaos. Only then does thermodynamics begin with its equations. As in physics or mathematics, we must have at least two different dimensions or values – distance, volume, area, force, speed, time, intensity, voltage, etc. Then we can compare, measure and solve. Then we can generalize and predict and verify by measurement, etc.
To have energy we must have at least two or more wavelenghts. Only one wavelenght there is no ratio – only one value equals to 1 (or anything else as we wish). The value of energy is given by ratio of measured energy to base unit for energy.
Conservation of energy (matter) is valid only for isolated space like in second law of thermodynamics. The sum of total energy before the experiment in isolated space is equal with the sum of total energy after the experiment.
The law of conservation energy or of conservation shapes or structures like pots or artworks at all. The law of conservation of information? The question is the category of space – open, closed or isolated space. There could be a change in the category of space in the universe.
Not only the law of conservation energy, but conservation of frequency or shapes, space, volume or artworks which are sometimes broken? Where is the point of view? What about the frequency. What does the frequency mean? Regular changes or nearly regular changes? See probabilistic distribution with peak in the middle. How long the frequency must to be or how many? Where is the point of view for valuating what is frequency, how many are there parts and so on. What about the part of frequency? Like the part of the pot which is created by the potter. Such laws are valid only for isolated space. And what does it mean the isolated space? Is it even possible to have that kind of space in the universe?
Where did the information come from? Where did all “regular” changes come from in such indescribable random cirmcumastances of quantum foam. new music songs, art works, inventions, new ideas, etc. The law of conservation of new music songs, art works, inventions, new ideas, etc. information? See entropy – informations, shapes and structures.
What does it mean the term Coherence?
Coherence is closely related to chaotic, ordered and by transition states. Coherence means bound chaos e.g. to a certain direction of movement. See the following distribution
1) free chaos withou any regularities, e.g. gas in closed box withou any inner flow
2) partial bound chaos with some regularities, e.g. turbulent flow
3) completely bound chaos, e.g. laminar flow or light amplification and stimulated emission of radiation
And thus we come to Quantum generators of coherent behavior like electromagnetic radiation, laser and maser, also like a coherent source of radio waves – LC oscillator, but also a coherent sources of laminar flow in chaotic liquids or gases in pipes, or a coherent source of mechanical motion such as a flying object or an oscillating pendulum.
But it is absolutely clear that without bonded thermal fluctuations (for example around the equilibrium position in solids) there would be no coherence, no coherent sources such as LC oscillators, quantum generators (masers and lasers) and for example in mechanics pendulums. Coherence is tightly connected with the open system vs. closed or isolated system in thermodynamic.
See the closed box in thermodynamics. See below
There are plenty particles of chaotically moving in varying levels of regularity.
From a global perspective (from the outside) we can roughly distinguish three basic levels:
1) complete chaos, pure randomness, it is impossible to determine the dominant direction of movement
2) partial chaos, the dominant direction of chaotic movement can be determined
3) complete order, where all particles move in the same direction (uniformly), without the slightest deviation from the direction of motion – this state is excluded in the real world, there will always be minimal but noticeable deviations out of the direction of the main motion.
Ad 2) – we can imagine the movement of electrons in metals. Free electrons are present in metals as a result of metallic bond. These electrons are not at rest but move chaotically with greater or lesser intensity (depending on temperature). Precisely, they move chaotically so that no electric current passes through the metal conductor. The situation changes when we connect a voltage – potential difference – electric field to both ends of the conductor. This field propagates at the speed of light. And it’s the potential difference that causes the electrons to move in a directed manner. Still the electrons will move chaotically, but with a predominant direction in the sense of the electric field (potential difference). However, the average speed of electrons in metal is low, cca hundredths of mm/s. This chaotic motion will proceed in the direction of the potential difference. Just as the chaotic flow of air molecules flows in the direction of the potential difference between two chaotic environments differing in their temperature (pressure). In short, the motion of electrons or air molecules is never ideally directed, but always chaotic with a predominant direction of motion.
We also need to distinguish between changes in the main (directed) direction of chaotic motion. In short – when the dominant direction of motion will change after some time. See the steam flow in the labyrinth plugs of turbines. Here the criterion applies – the change in the main motion must be greater than the original chaotic motion of the particles.
See thermodynamics
There are a large number of equations of state for real gases. These equations become more complicated the higher the accuracy required and the wider the range of pressures and temperatures we want to describe and the closer the real gas state is to the critical point.
In the beginning we have chaos – the gases expand as they want, one more, one less, each time differently – at first sight we have no chance to describe the behaviour of the gases.
A few scientists (Boyle, Mariott, Gay, Lussac, Pascal, Torriceli, … ) start to take a closer look at the behavior of the gases. They enclose the gases in containers with a piston, measure (using their chosen units of temperature) what has changed (temperature, pressure, volume), isolate the gases from their surroundings and behold very simple elementary math formulas come out.
pV = nRT where p-pressure, V-volume, T-temperature, R-gas constant
After next time, we find when we go into detail that the calculated values differ. Let’s refine our equations with more measurements. We get more complex formulas – not so simple.
van der Waals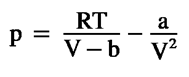
not mentioned constant a, b.
And if we go into even more detail – we have a choice – very complex formulas with a certain accuracy for a given region of physical conditions we obtain the BWR equation (Benedict, Webb and Rubin)![]()
In the beginning there is a chaos of the gases behaviour. In the first time there is a pretty simple and beautiful equation for ideal gases. In the middle there is quite complicated but also beauty equation. In the end there is an chaos of very complicated equation which are valid for very narrow range of pressures and temperatures. There is again a chaos, but in descriptiveness. See a curve below.
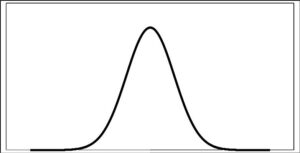
chaos equations over-describe,
In summary: The more the equation describing the physical process is more general the more beautiful such equation is and vice versa the more concrete equation is the more its beauty decreases. Thus, beautiful equations have a wide range of validity with poor accuracy and less beautiful equations have a very limited range of validity with high accuracy. The simple thermodynamic equation of state is not applicable in practice. Respectively it is applicable, but as a very inaccurate view and even for light gases such as hydrogen, helium. When using the Van der Waals equation, the situation is better. Furthermore, we use specialized equations with a defined interval of their validity. Example from practice – calculation of a circuited hot water network (not mention a circuited steam network) – even if we use the best equations, as accurately as possible, if we specify the appropriate water values for the given conditions – we still get only frame results. And the hot water network has to be finely regulated in practice.
In other words – without measurement and control, technical processes are not possible in practice. Just by equations we can set a given range, but without external regulatory interventions the function of hot water systems, steam power plants, rockets and in general all technical infrastructure is impossible. In the same way it is impossible to accurately predict the behaviour of billiars balls after n-collisions. Not to mention legendary three body problem formulated by H. Poincare
This is what makes the engineering interesting. The situation is different every time, even if the calculations show the same results. You still need to respond differently. There’s always something to discover, like in science. There are always new adventures of experience until Infinity.
Summary: Thermodynamic processes served in their time as the basis for the derivation not only of entropy, but of all considerations of energy and, in fact, of the behaviour of the whole universe. When the basis is the same, it is hard to believe that the description of the thermodynamics of a collapsing star, or processes in dust nebulae, processes in star-gas systems, etc., that these processes will proceed ideally according to framework calculations as opposed to difficult (mostly iterative) calculations of the motion of three bodies, or processes in steam systems, or in the production of artificial diamonds, etc. It is hardly possible to predict the future evolution of the universe on the basis of idealized quantum mechanical equations together with the equations of general relativity. And vice versa to accurately document the history of the universe up to now.
The very interesting thermodynamic process – isothermal expansion of an ideal gas
At the beginning of such process there is the ideal gas with its characteristics as temperature T, pressure P , volume V, energy U, number of particles N, density D, entropy S. We will examine this process in detail in terms of the base units – the definition of distance (volume), pressure and temperature. At the beginning of the isothermal expansion there is an initial state with following values of T1, P1, V1, U1, N1, D1, S1
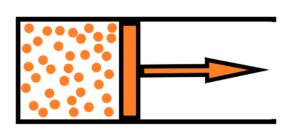
in the end of the isothermal expansion there is a final state with following values of T2, P2, V2, U2, N2, D2, S2

T1 = T2, P1 > P2, V1 < V2, U1 = U2, N1 = N2, D1 > D2, S1 < S2. The temperature is constant as well as the internal energy and numbering of particles, of course. The pressure after expansion decreased, as well as the density, which are both connected. On the contrary, the volume has increased along with the entropy, which are both again connected. The internal energy of expanding gas – it is constant. Throughout the isothermal process, the reduction of internal energy is compensated by the supply of thermal energy from the outside. Which means that 100% of the supplied external thermal energy is converted into mechanical work. The chaotic behavior of the ideal gas molecules is converted into a directed movement of the piston in a given direction, with the efficiency of 100 %. At first it looks amazing, but we need to go further. See pressure reduction together with volume increase, Thus a change in the ordering of the possible states of the gas molecules – the entropy. The adiabatic expansion also converts the internal energy of the chaotic ideal gas into useful work of the directed piston motion. But not with 100% efficiency. Then, if there were to be 100% efficiency, the internal energy of the gas would have to drop to 0 – in short, the gas temperature would have to be 0 Kelvin – which is impossible.
It is good to remind and discuss the experiment with the compression or expansion of electromagnetic radiation enclosed in a box (mirrors, for example). The so-called Einstein experiment. When the box is compressed, the wavelength of e.g. light is reduced, so the frequency f is increased, which means an increase of energy E = hf. The increase of the energy of the enclosed radiation is at the expense of the work supplied from the outside in compressing the box.
It is good to remind and discuss the experiment with the compression or expansion of electromagnetic radiation enclosed in a box (mirrors, for example). The so-called Einstein experiment. When the box is compressed, the wavelength of e.g. light is reduced, so the frequency f is increased, which means an increase of its energy E = h*f, where h is Planck´constant. The increase of the energy of the enclosed radiation is at the expense of the work supplied from the outside in compressing the box. See below an initial state wit enclosed wavelenght with initial energy E1 = h*f1
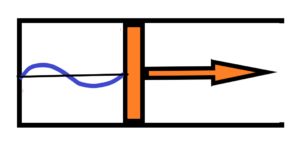
after expansion the wavelenght in the closed box will be longer, there will bel longer wavelenght with lower frequency which means lower energy E2 = h*f2 – see below
This makes it very easy to demonstrate isothermal and adiabatic expansion of radiation. In adiabatic radiation expansion, the situation is simple – the wavelength becomes longer, the frequency and thus the energy becomes lower. The longer the wavelength expansion, the greater the efficiency. 100% efficiency is unreachable – the wavelength would have to be extended to infinity, i.e. the frequency would be reduced to zero.
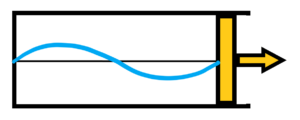
But the situation is different in the case of isothermal expansion. Here the wavelength and therefore the energy remains constant. Space is becoming longer, but the wavelength is still constant. Which is possible if the decrease in frequency (wavelength expansion) is supplied from the outside so that the frequency and hence the wavelength remains constant. But that’s a contradiction in terms. For the wavelength of radiation to remain the same at a given extension, it means moving the piston of the enclosed space a distance equal to the wavelength. So there will be two wavelengths in the enclosed space. Or three, or four, … or x, depending on how many wavelength periods there were to begin with. See below – initial state for expansion
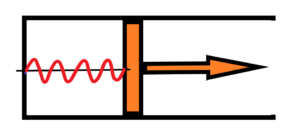
In the inital state there are four periods f1 of radiation oscillation. There are two courses of thermal expansion – adiabatic or isothermal.
Firstly the adiabatic expansion. The final state for the adiabatic expansion – see below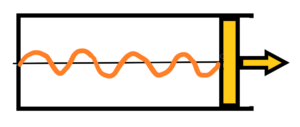
After the end of adiabatic expansion there are again four periods, but with longer wavelength and lower frequency h2. The difference in energy E1before and after E2 the expansion is equal to the work A done by the piston. A = E1 – E2 = hf1 – hf2 = h (f1-f2). Part of the radiation energy was used for the work A done by the piston. The longer the path of the expanding piston under the pressure of the radiation, the lower the energy (frequency) of the radiation enclosed in the cylinder. It sounds logical. But go on to the isothermal expansion of radiation.
The final state for the isothermal expansion – see below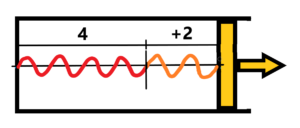
We see that there has been the addition from four to six of periods. Somewhere from the outside. Thus, the enclosed frequency remains constant. What about the work done by the piston? The radiation energy in the cylinder is constant, there is no reduction. The energy is still equal to E = hf. What work A did the piston make during a move of a distance of two periods? The energy E of radiation is constant!
By the way. Imagine a moving ball in the same closed space – the cylinder with the piston inside that. Such ball has kinetic energy Ek. If it is an adiabatic expansion, the kinetic energy Ek of the ball is reduced at the cost of the work A done by the piston. If it is an isothermal expansion, then the kinetic energy Ek of the ball remains constant – because it is kept on the same level by supply the energy Es from the outside. Es = A. There is a decrease in the kinetic energy of the ball, but its energy is restored to its original amount from the outside. The velocity of the ball will be the same after the isothermal expansion. It is the same with the isothermal expansion of radiation. As the radiation expands, its energy decreases. It depends on the piston displacement. That’s the work done by the piston. But the frequency of the enclosed radiation is from the outside returned to its original level – before the expansion.
Go back to isothermal expansion of enclosed radiation. It is interesting that the change of the piston position in the case of isothermal expansion takes place in steps equal to the wavelength of the enclosed radiation. Or the piston may move by distances equal to multiples of the wavelength of the enclosed radiation. The piston has allowed states, allowed positions, allowed distances. In the case of an intermediate position is not an isothermal expansion. See allowed positions of electron orbitals.
There is a prolongation of the enclosed radiation during the isothermal expansion. The frequency is constant during the “jump” or quantum expansion, but there are many more wavelengths, which leads us to another interesting question about expansion or changes in spacetime in general.
Let´s imagin the following thinking experiment. No adiabatic expansion, but adiabatic compression of radiation in closed box. To adiabatically compress radiation from outside then we need to supply the work dA. The energy of radiation inccrease to dE = h*df = dA. That’s fine, the change in frequency and therefore the energy of the radiation is equal to the work dA supplied. But suppose we want to compress the radiation to a wavelength close to zero, i.e. the frequency and hence the energy will increase towards infinity. How to do that? Where to find in the world, in the universe, a force so powerful? It is most likely to be found in a collapsing very massive star where the thermonuclear reaction stops and there is nothing to balance the gravitational force. Since we are on a thought experiment, there will be an empty space inside the collapsar filled with enclosed radiation. See below
A collapsing massive star goes into the neutron star stage. And the enclosed radiation must be compressed with enormous force. But what is the power of the gravitational field inside the star? Maximal or minimal? The intensity in the center of such star is exactly equal to zero. We know from classical mechanics that the gravitational effect is zero in the middle of an ideal spherical body with any mass. Even if the mass weighs hundreds of thousands of medium-sized stars. The radiation inside such a massive star, a neutron star, is gravitationally isolated from the neutron star. See below the intensity K and potential U of the gravitational field inside and near a very massive ball.
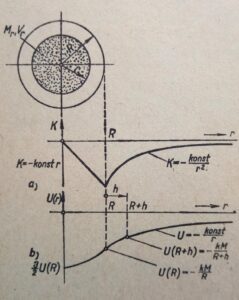
Why do I write down these articles, these reflections? Because the above gravitational intensity and potential profiles are derived from idealized models where we assume a continuous gravitational force. Infinitesimal calculus – differential equations. But gravity cannot be continuous – it does have its bearers. That bearers are grouped atoms, or then particles (neutrons) at close distances. The grouped excitations of the quantum field. But what do we know about such tight excitations? Are they even possible from our perspective of sparse densities compared to the density of a neutron star? Or how does the quantum field behave in such a massive star? However, this massive star, even if it collapses, is the result of a quantum field. Does that mean the quantum field is collapsing as well? Would the effect be stronger than the cause? We don´t know the origin of quantum excitations so-called waves-particles.
Matter needs a space, a space time, witthout space there is no matter, no time, no fluctuations however small they may be. Matter is space and time, just as space is matter and time, and time is matter and space (one cannot exist without the second and the third). If and only if matter is compressed into extremely small dimensions in the middle, this could mean an extreme increase in exchange reactions (frequency) and thus the energy of such a piece of matter could be higher than the whole universe.
But go on! When the collapsing star begins to approach the black star stage (called a black hole) the energy of the compressed radiation will be greater than the energy of the star itself, and on further compression the enclosed radiation will have such a short wavelength – almost infinitesimal – that its energy will be greater than the energy of our entire universe. See below
All we need to do is fit the upper equations mathematically. Not to mention the energy of the collapsing star. By the way, time slows down dramatically in the immediate surroundings of a neutron star. So a star, if we respect general relativity, cannot, in the time of our universe, collapse into a black hole. From our point of view, the collapse “freezes”.
Gravity needs space. Just like every field excitation, just like every property needs space. Without space, there is neither matter nor time. Just as time does not exist outside of matter and space.
Thus, it is at most likely that a collapsing star will return to its initial state – the basic fluctuating excitations of an omnipresent quantum field. But verification is beyond our limits.
See hydrodynamics – continuity equation, so-called the law of conservation of volume flow capacity S1v1 = S2v2 , where S is the area of the pipe and v is the velocity inside such pipe, in different cross-sections the total flow is kept – the larger the pipe cross-section the lower the velocity and vice versa – sure, this equation is “valid”, but only for an ideal state that does not exist in the real world. For the ideal isolated system without any inlunces from outside or inside – such a state is impossible by the nature of real nature, where everything is related to everything, of course with different influenceability.If I appropriately substitute into the previously mentioned equation I get supersonic or even supra-light values.
Blackbody radiation is well evaluated by devices. See increasing frequency of emitted light radiation versus e.g. photoelectric effect. But the color of the emitted radiation is evaluated only by man, or by people with different levels of sensitivity to light. See below![]()
No machine in the world can evaluate the colour of the emitted radiation. Well, it does, but the range of colors must be input into the device by a human based on a color perception scale.
… to be continued
See below – brief remarks waiting for word processing to articels
| Download | Download | Download | Download | |
| Spring_collisions | Thermodynamics | Energy_conversion | gravity_contemplation | |
| Origin energy_I | ||||
| Origin_waves | ||||
